ראשית, נבין את עץ בינארי ו עץ חיפוש בינארי בנפרד, ולאחר מכן נבחן את ההבדלים בין עץ בינארי לעץ חיפוש בינארי.
מהו עץ בינארי?
א עץ בינארי הוא
העץ הבינארי יכול להיות מיוצג כך:
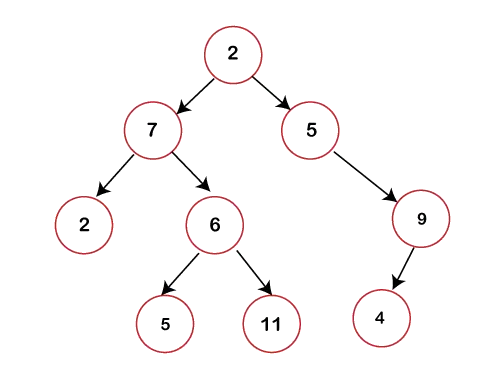
באיור לעיל, אנו יכולים לראות שכל צומת מכיל 2 ילדים לכל היותר. אם צומת כלשהו אינו מכיל ילד שמאלי או ימני אז הערך של המצביע ביחס לאותו ילד יהיה NULL.
מינוחים בסיסיים המשמשים בעץ בינארי הם:
בעץ בינארי, יש עץ אחד המכונה א עץ בינארי מושלם . זה עץ שבו כל הצמתים הפנימיים חייבים להכיל שני צמתים, וכל צמתי העלים חייבים להיות באותו עומק. במקרה של עץ בינארי מושלם, ניתן לחשב את המספר הכולל של צמתים בעץ בינארי באמצעות המשוואה הבאה:
n = 2m+1-1
כאשר n הוא מספר הצמתים, m הוא עומק הצומת.
מהו עץ חיפוש בינארי?
א עץ חיפוש בינארי הוא עץ שעוקב אחר סדר כלשהו כדי לסדר את האלמנטים, ואילו העץ הבינארי אינו עוקב אחר שום סדר. בעץ חיפוש בינארי, הערך של הצומת השמאלי חייב להיות קטן מהצומת האב, והערך של הצומת הימני חייב להיות גדול מהצומת האב.
בואו נבין את הרעיון של עץ חיפוש בינארי באמצעות דוגמאות.

באיור לעיל, אנו יכולים לראות שהערך של צומת השורש הוא 15, שהוא גדול מהערך של כל הצמתים בתת-העץ השמאלי. הערך של צומת שורש קטן מהערכים של כל הצמתים בתת-עץ ימני. כעת, אנו עוברים לילד השמאלי של צומת השורש. 10 גדול מ-8 וקטן מ-12; הוא גם מספק את המאפיין של עץ החיפוש הבינארי. כעת, אנו עוברים לילד הימני של צומת השורש; הערך 20 גדול מ-17 וקטן מ-25; זה גם עונה על המאפיין של עץ החיפוש הבינארי. לכן, אנו יכולים לומר שהעץ המוצג לעיל הוא עץ החיפוש הבינארי.
כעת, אם נשנה את הערך של 12 ל-16 בעץ הבינארי לעיל, עלינו למצוא אם הוא עדיין עץ חיפוש בינארי או לא.

הערך של צומת השורש הוא 15 שהוא גדול מ-10 אך קטן מ-16, כך שהוא אינו עונה על המאפיין של עץ החיפוש הבינארי. לכן, זה לא עץ חיפוש בינארי.
פעולות על עץ חיפוש בינארי
אנו יכולים לבצע פעולות הוספה, מחיקה וחיפוש בעץ החיפוש הבינארי. בואו נבין כיצד מתבצע חיפוש בחיפוש בינארי. העץ הבינארי מוצג להלן שעליו עלינו לבצע את פעולת החיפוש:

נניח שעלינו לחפש 10 בעץ הבינארי לעיל. כדי לבצע את החיפוש הבינארי, נשקול את כל המספרים השלמים במערך ממוין. ראשית, אנו יוצרים רשימה מלאה במרחב חיפוש, וכל המספרים יהיו קיימים במרחב החיפוש. מרחב החיפוש מסומן על ידי שני מצביעים, כלומר, התחלה וסיום. ניתן לייצג את המערך של העץ הבינארי לעיל

ראשית, נחשב את האלמנט האמצעי ונשווה את האלמנט האמצעי לאלמנט שאותו יש לחפש. האלמנט האמצעי מחושב באמצעות n/2. הערך של n הוא 7; לכן, האלמנט האמצעי הוא 15. האלמנט האמצעי אינו שווה לאלמנט המחפש, כלומר 10.
הערה: אם האלמנט שמחפשים הוא קטן מהאלמנט האמצעי, החיפוש יתבצע בחצי השמאלי; אחרת, החיפוש יתבצע בחצי הימני. במקרה של שוויון נמצא היסוד.
מכיוון שהאלמנט שיש לחפש קטן מהאלמנט האמצעי, כך החיפוש יתבצע במערך השמאלי. כעת החיפוש מצטמצם לחצי, כפי שמוצג להלן:

האלמנט האמצעי במערך השמאלי הוא 10, השווה לאלמנט המחפש.
מורכבות הזמן
בחיפוש בינארי, ישנם n אלמנטים. אם האלמנט האמצעי אינו שווה לאלמנט המחפש, אז מרחב החיפוש מצטמצם ל-n/2, ונמשיך להקטין את מרחב החיפוש ב-n/2 עד שנמצא את האלמנט. בכל ההפחתה, אם נעבור מ-n ל-n/2 ל-n/4 וכן הלאה, אז זה ייקח לוג2n צעדים.
הבדלים בין עץ בינארי לעץ חיפוש בינארי

| בסיס להשוואה | עץ בינארי | עץ חיפוש בינארי |
|---|---|---|
| הַגדָרָה | עץ בינארי הוא מבנה נתונים לא ליניארי שבו לצומת יכולים להיות שני ילדים לכל היותר, כלומר, לצומת יכולים להיות 0, 1 או מקסימום שני ילדים. עץ חיפוש בינארי הוא עץ בינארי מסודר שבו מתבצע סדר מסוים כדי לארגן את הצמתים בעץ. | |
| מִבְנֶה | המבנה של העץ הבינארי הוא שהצומת הראשון או הצומת העליון ידוע כצומת השורש. כל צומת בעץ בינארי מכיל את המצביע השמאלי ואת המצביע הימני. המצביע השמאלי מכיל את הכתובת של תת העץ השמאלי, ואילו המצביע הימני מכיל את הכתובת של תת העץ הימני. | עץ החיפוש הבינארי הוא אחד מסוגי העץ הבינארי שערך כל הצמתים בתת-עץ השמאלי קטן או שווה לצומת השורש, והערך של כל הצמתים בתת-עץ ימני גדול או שווה ל- הערך של צומת השורש. |
| פעולות | הפעולות שניתן ליישם על עץ בינארי הן הכנסה, מחיקה ומעבר. | עצי חיפוש בינאריים הם העצים הבינאריים הממוינים המספקים הכנסה, מחיקה וחיפוש מהירים. חיפושים מיישמים בעיקר חיפוש בינארי שכן כל המפתחות מסודרים בסדר ממוין. |
| סוגים | ארבעה סוגים של עצים בינאריים הם עץ בינארי מלא, עץ בינארי מלא, עץ בינארי מושלם ועץ בינארי מורחב. | ישנם סוגים שונים של עצי חיפוש בינאריים כגון עצי AVL, Splay tree, עצי טנגו וכו'. |
