במאמר זה, נדון בעץ החיפוש הבינארי. מאמר זה יהיה מאוד מועיל ואינפורמטיבי לסטודנטים בעלי רקע טכני מכיוון שהוא נושא חשוב בקורס שלהם.
לפני שנעבור ישירות לעץ החיפוש הבינארי, בואו נראה תחילה תיאור קצר של העץ.
מה זה עץ?
עץ הוא מעין מבנה נתונים המשמש לייצוג הנתונים בצורה היררכית. זה יכול להיות מוגדר כאוסף של אובייקטים או ישויות הנקראים כצמתים המקושרים יחד כדי לדמות היררכיה. עץ הוא מבנה נתונים לא ליניארי מכיוון שהנתונים בעץ אינם מאוחסנים באופן ליניארי או ברצף.
עכשיו, בואו נתחיל את הנושא, עץ החיפוש הבינארי.
מהו עץ חיפוש בינארי?
עץ חיפוש בינארי עוקב אחר סדר מסוים כדי לסדר את האלמנטים. בעץ חיפוש בינארי, הערך של הצומת השמאלי חייב להיות קטן מהצומת האב, והערך של הצומת הימני חייב להיות גדול מהצומת האב. כלל זה מוחל באופן רקורסיבי על תת-העץ השמאלי והימני של השורש.
בואו נבין את הרעיון של עץ חיפוש בינארי בעזרת דוגמה.
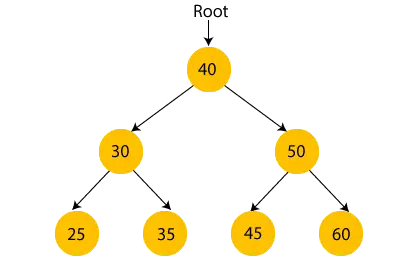
באיור לעיל, אנו יכולים לראות שצומת השורש הוא 40, וכל הצמתים של תת-העץ השמאלי קטנים יותר מצומת השורש, וכל הצמתים של תת-העץ הימני גדולים יותר מצמת השורש.
באופן דומה, אנו יכולים לראות שהילד השמאלי של צומת השורש גדול מהילד השמאלי שלו וקטן מהילד הימני שלו. אז, זה גם עונה על המאפיין של עץ החיפוש הבינארי. לכן, אנו יכולים לומר שהעץ בתמונה למעלה הוא עץ חיפוש בינארי.
נניח שאם נשנה את הערך של צומת 35 ל-55 בעץ שלמעלה, בדוק אם העץ יהיה עץ חיפוש בינארי או לא.

בעץ הנ'ל, הערך של צומת השורש הוא 40, שהוא גדול מהילד השמאלי שלו 30 אבל קטן מהילד הימני של 30, כלומר, 55. לכן, העץ הנ'ל אינו מספק את המאפיין של עץ החיפוש הבינארי. לכן, העץ הנ'ל אינו עץ חיפוש בינארי.
יתרונות עץ החיפוש הבינארי
- חיפוש אלמנט בעץ החיפוש הבינארי הוא קל מכיוון שתמיד יש לנו רמז לאיזה תת-עץ יש את האלמנט הרצוי.
- בהשוואה למערך ולרשימות מקושרות, פעולות ההכנסה והמחיקה מהירות יותר ב-BST.
דוגמה ליצירת עץ חיפוש בינארי
כעת, בואו נראה את היצירה של עץ חיפוש בינארי באמצעות דוגמה.
נניח שרכיבי הנתונים הם - 45, 15, 79, 90, 10, 55, 12, 20, 50
- ראשית, עלינו להכניס ארבע חמש לתוך העץ כשורש העץ.
- לאחר מכן, קרא את האלמנט הבא; אם הוא קטן יותר מצומת השורש, הכנס אותו כשורש של תת-העץ השמאלי, ועבור לאלמנט הבא.
- אחרת, אם האלמנט גדול יותר מצומת השורש, הכנס אותו כשורש של תת-העץ הימני.
כעת, בואו נראה את התהליך של יצירת עץ החיפוש הבינארי באמצעות אלמנט הנתונים הנתון. תהליך יצירת ה-BST מוצג להלן -
שלב 1 - הכנס 45.

שלב 2 - הכנס 15.
מכיוון ש-15 קטן מ-45, אז הכנס אותו כצומת השורש של תת-העץ השמאלי.

שלב 3 - הכנס 79.
מכיוון ש-79 גדול מ-45, אז הכנס אותו כצומת השורש של תת-העץ הימני.

שלב 4 - הכנס 90.
90 גדול מ-45 ו-79, אז הוא יוכנס כתת-העץ הימני של 79.

שלב 5 - הכנס 10.
10 קטן מ-45 ו-15, ולכן הוא יוכנס כתת-עץ שמאלי של 15.

שלב 6 - הכנס 55.
55 גדול מ-45 וקטן מ-79, אז הוא יוכנס כתת-העץ השמאלי של 79.

שלב 7 - הכנס 12.
12 קטן מ-45 ו-15 אבל גדול מ-10, אז הוא יוכנס כתת-העץ הימני של 10.

שלב 8 - הכנס 20.
20 קטן מ-45 אך גדול מ-15, ולכן הוא יוכנס כתת-העץ הימני של 15.

שלב 9 - הכנס 50.
50 גדול מ-45 אך קטן מ-79 ו-55. לכן, הוא יוכנס כתת-עץ שמאלי של 55.

כעת הושלמה יצירת עץ החיפוש הבינארי. לאחר מכן, בואו נעבור לפעולות שניתן לבצע בעץ החיפוש הבינארי.
אנו יכולים לבצע פעולות הוספה, מחיקה וחיפוש בעץ החיפוש הבינארי.
בואו נבין כיצד מתבצע חיפוש בעץ חיפוש בינארי.
חיפוש בעץ חיפוש בינארי
חיפוש פירושו למצוא או לאתר אלמנט או צומת ספציפיים במבנה נתונים. בעץ החיפוש הבינארי, החיפוש בצומת קל מכיוון שאלמנטים ב-BST מאוחסנים בסדר מסוים. השלבים של חיפוש צומת בעץ החיפוש הבינארי מפורטים כדלקמן -
- ראשית, השווה את האלמנט שיש לחפש עם אלמנט השורש של העץ.
- אם השורש מותאם לאלמנט היעד, החזר את מיקום הצומת.
- אם הוא לא מותאם, בדוק אם הפריט קטן מאלמנט השורש, אם הוא קטן מאלמנט השורש, אז עברו לעץ המשנה השמאלי.
- אם הוא גדול יותר מאלמנט השורש, עבור אל תת-העץ הימני.
- חזור על ההליך לעיל באופן רקורסיבי עד למציאת ההתאמה.
- אם האלמנט לא נמצא או אינו קיים בעץ, החזר NULL.
כעת, בואו נבין את החיפוש בעץ בינארי באמצעות דוגמה. אנחנו לוקחים את עץ החיפוש הבינארי שנוצר למעלה. נניח שעלינו למצוא את צומת 20 מהעץ למטה.
שלב 1:
סוג משתנים java

שלב 2:

שלב 3:

כעת, בואו נראה את האלגוריתם לחיפוש אלמנט בעץ החיפוש הבינארי.
אלגוריתם לחיפוש אלמנט בעץ החיפוש הבינארי
Search (root, item) Step 1 - if (item = root → data) or (root = NULL) return root else if (item <root 2 → data) return search(root left, item) else right, end if step - < pre> <p>Now let's understand how the deletion is performed on a binary search tree. We will also see an example to delete an element from the given tree.</p> <h3>Deletion in Binary Search tree</h3> <p>In a binary search tree, we must delete a node from the tree by keeping in mind that the property of BST is not violated. To delete a node from BST, there are three possible situations occur -</p> <ul> <li>The node to be deleted is the leaf node, or,</li> <li>The node to be deleted has only one child, and,</li> <li>The node to be deleted has two children</li> </ul> <p>We will understand the situations listed above in detail.</p> <p> <strong>When the node to be deleted is the leaf node</strong> </p> <p>It is the simplest case to delete a node in BST. Here, we have to replace the leaf node with NULL and simply free the allocated space.</p> <p>We can see the process to delete a leaf node from BST in the below image. In below image, suppose we have to delete node 90, as the node to be deleted is a leaf node, so it will be replaced with NULL, and the allocated space will free.</p> <img src="//techcodeview.com/img/ds-tutorial/58/binary-search-tree-15.webp" alt="Binary Search tree"> <p> <strong>When the node to be deleted has only one child</strong> </p> <p>In this case, we have to replace the target node with its child, and then delete the child node. It means that after replacing the target node with its child node, the child node will now contain the value to be deleted. So, we simply have to replace the child node with NULL and free up the allocated space.</p> <p>We can see the process of deleting a node with one child from BST in the below image. In the below image, suppose we have to delete the node 79, as the node to be deleted has only one child, so it will be replaced with its child 55.</p> <p>So, the replaced node 79 will now be a leaf node that can be easily deleted.</p> <img src="//techcodeview.com/img/ds-tutorial/58/binary-search-tree-16.webp" alt="Binary Search tree"> <p> <strong>When the node to be deleted has two children</strong> </p> <p>This case of deleting a node in BST is a bit complex among other two cases. In such a case, the steps to be followed are listed as follows -</p> <ul> <li>First, find the inorder successor of the node to be deleted.</li> <li>After that, replace that node with the inorder successor until the target node is placed at the leaf of tree.</li> <li>And at last, replace the node with NULL and free up the allocated space.</li> </ul> <p>The inorder successor is required when the right child of the node is not empty. We can obtain the inorder successor by finding the minimum element in the right child of the node.</p> <p>We can see the process of deleting a node with two children from BST in the below image. In the below image, suppose we have to delete node 45 that is the root node, as the node to be deleted has two children, so it will be replaced with its inorder successor. Now, node 45 will be at the leaf of the tree so that it can be deleted easily.</p> <img src="//techcodeview.com/img/ds-tutorial/58/binary-search-tree-17.webp" alt="Binary Search tree"> <p>Now let's understand how insertion is performed on a binary search tree.</p> <h3>Insertion in Binary Search tree</h3> <p>A new key in BST is always inserted at the leaf. To insert an element in BST, we have to start searching from the root node; if the node to be inserted is less than the root node, then search for an empty location in the left subtree. Else, search for the empty location in the right subtree and insert the data. Insert in BST is similar to searching, as we always have to maintain the rule that the left subtree is smaller than the root, and right subtree is larger than the root.</p> <p>Now, let's see the process of inserting a node into BST using an example.</p> <img src="//techcodeview.com/img/ds-tutorial/58/binary-search-tree-18.webp" alt="Binary Search tree"> <br> <img src="//techcodeview.com/img/ds-tutorial/58/binary-search-tree-19.webp" alt="Binary Search tree"> <h3>The complexity of the Binary Search tree</h3> <p>Let's see the time and space complexity of the Binary search tree. We will see the time complexity for insertion, deletion, and searching operations in best case, average case, and worst case.</p> <h3>1. Time Complexity</h3> <table class="table"> <tr> <th>Operations</th> <th>Best case time complexity</th> <th>Average case time complexity</th> <th>Worst case time complexity</th> </tr> <tr> <td> <strong>Insertion</strong> </td> <td>O(log n)</td> <td>O(log n)</td> <td>O(n)</td> </tr> <tr> <td> <strong>Deletion</strong> </td> <td>O(log n)</td> <td>O(log n)</td> <td>O(n)</td> </tr> <tr> <td> <strong>Search</strong> </td> <td>O(log n)</td> <td>O(log n)</td> <td>O(n)</td> </tr> </table> <p>Where 'n' is the number of nodes in the given tree.</p> <h3>2. Space Complexity</h3> <table class="table"> <tr> <th>Operations</th> <th>Space complexity</th> </tr> <tr> <td> <strong>Insertion</strong> </td> <td>O(n)</td> </tr> <tr> <td> <strong>Deletion</strong> </td> <td>O(n)</td> </tr> <tr> <td> <strong>Search</strong> </td> <td>O(n)</td> </tr> </table> <ul> <li>The space complexity of all operations of Binary search tree is O(n).</li> </ul> <h2>Implementation of Binary search tree</h2> <p>Now, let's see the program to implement the operations of Binary Search tree.</p> <p> <strong>Program:</strong> Write a program to perform operations of Binary Search tree in C++.</p> <p>In this program, we will see the implementation of the operations of binary search tree. Here, we will see the creation, inorder traversal, insertion, and deletion operations of tree.</p> <p>Here, we will see the inorder traversal of the tree to check whether the nodes of the tree are in their proper location or not. We know that the inorder traversal always gives us the data in ascending order. So, after performing the insertion and deletion operations, we perform the inorder traversal, and after traversing, if we get data in ascending order, then it is clear that the nodes are in their proper location.</p> <pre> #include using namespace std; struct Node { int data; Node *left; Node *right; }; Node* create(int item) { Node* node = new Node; node->data = item; node->left = node->right = NULL; return node; } /*Inorder traversal of the tree formed*/ void inorder(Node *root) { if (root == NULL) return; inorder(root->left); //traverse left subtree cout<data <right); traverse right subtree } node* findminimum(node* cur) *to find the inorder successor* { while(cur->left != NULL) { cur = cur->left; } return cur; } Node* insertion(Node* root, int item) /*Insert a node*/ { if (root == NULL) return create(item); /*return new node if tree is empty*/ if (item data) root->left = insertion(root->left, item); else root->right = insertion(root->right, item); return root; } void search(Node* &cur, int item, Node* &parent) { while (cur != NULL && cur->data != item) { parent = cur; if (item data) cur = cur->left; else cur = cur->right; } } void deletion(Node*& root, int item) /*function to delete a node*/ { Node* parent = NULL; Node* cur = root; search(cur, item, parent); /*find the node to be deleted*/ if (cur == NULL) return; if (cur->left == NULL && cur->right == NULL) /*When node has no children*/ { if (cur != root) { if (parent->left == cur) parent->left = NULL; else parent->right = NULL; } else root = NULL; free(cur); } else if (cur->left && cur->right) { Node* succ = findMinimum(cur->right); int val = succ->data; deletion(root, succ->data); cur->data = val; } else { Node* child = (cur->left)? cur->left: cur->right; if (cur != root) { if (cur == parent->left) parent->left = child; else parent->right = child; } else root = child; free(cur); } } int main() { Node* root = NULL; root = insertion(root, 45); root = insertion(root, 30); root = insertion(root, 50); root = insertion(root, 25); root = insertion(root, 35); root = insertion(root, 45); root = insertion(root, 60); root = insertion(root, 4); printf('The inorder traversal of the given binary tree is -
'); inorder(root); deletion(root, 25); printf('
After deleting node 25, the inorder traversal of the given binary tree is -
'); inorder(root); insertion(root, 2); printf('
After inserting node 2, the inorder traversal of the given binary tree is -
'); inorder(root); return 0; } </data></pre> <p> <strong>Output</strong> </p> <p>After the execution of the above code, the output will be -</p> <img src="//techcodeview.com/img/ds-tutorial/58/binary-search-tree-20.webp" alt="Binary Search tree"> <p>So, that's all about the article. Hope the article will be helpful and informative to you.</p> <hr></root> תְפוּקָה
לאחר ביצוע הקוד לעיל, הפלט יהיה -

אז, זה הכל לגבי המאמר. מקווה שהמאמר יהיה מועיל ואינפורמטיבי עבורך.
