עלות מינימלית לחיתוך לוח לריבועים

נסה את זה ב-GfG Practice עלות מינימלית לחיתוך לוח לריבועים' title=

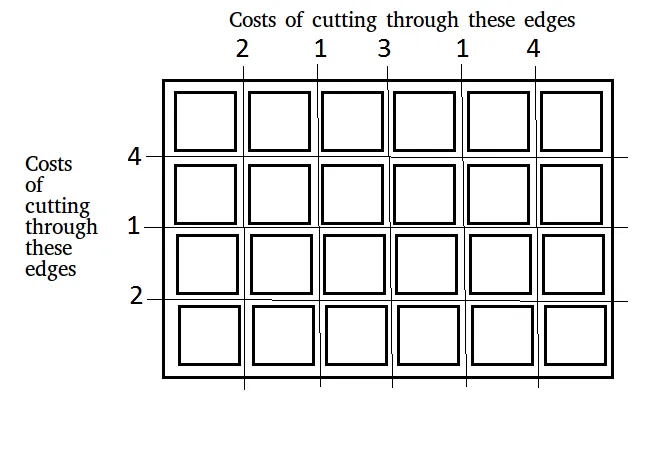
נתון לוח מידות n × מ' שצריך לחתוך ל-n × מ' ריבועים. העלות של ביצוע חיתוך לאורך קצה אופקי או אנכי מסופקת בשני מערכים:

x[] : חיתוך עלויות לאורך הקצוות האנכיים (לאורך).
ו[] : חיתוך עלויות לאורך הקצוות האופקיים (לרוחב).

מצא את העלות הכוללת המינימלית הנדרשת כדי לחתוך את הלוח לריבועים בצורה מיטבית.

דוגמאות:

קֶלֶט: x[] = [2 1 3 1 4] y[] = [4 1 2] n = 4 מ' = 6
תְפוּקָה: 42
הֶסבֵּר:

בתחילה לא. של מקטעים אופקיים = 1 & לא. של מקטעים אנכיים = 1.
הדרך האופטימלית לחתוך לריבוע היא:
בחר 4 (מ-x) -> חיתוך אנכי עלות = 4 × מקטעים אופקיים = 4
כעת מקטעים אופקיים = 1 מקטע אנכי = 2.
בחר 4 (מ-y) -> חיתוך אופקי עלות = 4 × מקטעים אנכיים = 8
כעת קטעים אופקיים = 2 קטעים אנכיים = 2.
בחר 3 (מ-x) -> חיתוך אנכי עלות = 3 × מקטעים אופקיים = 6
כעת מקטעים אופקיים = 2 מקטעים אנכיים = 3.
בחר 2 (מ-x) -> חיתוך אנכי עלות = 2 × מקטעים אופקיים = 4
כעת קטעים אופקיים = 2 קטעים אנכיים = 4.
בחר 2 (מ-y) -> חיתוך אופקי עלות = 2 × מקטעים אנכיים = 8
כעת מקטעים אופקיים = 3 מקטעים אנכיים = 4.
בחר 1 (מ-x) -> חיתוך אנכי עלות = 1 × מקטעים אופקיים = 3
כעת מקטעים אופקיים = 3 מקטעים אנכיים = 5.
בחר 1 (מ-x) -> חיתוך אנכי עלות = 1 × מקטעים אופקיים = 3
כעת מקטעים אופקיים = 3 מקטעים אנכיים = 6.
בחר 1 (מ-y) -> חיתוך אופקי עלות = 1 × מקטעים אנכיים = 6
כעת מקטעים אופקיים = 4 מקטעים אנכיים = 6.
אז העלות הכוללת = 4 + 8 + 6 + 4 + 8 + 3 + 3 + 6 = 42.
קֶלֶט: x[] = [1 1 1] y[] = [1 1 1] n = 4 מ' = 4
תְפוּקָה: 15
הֶסבֵּר:
בתחילה לא. של מקטעים אופקיים = 1 & לא. של מקטעים אנכיים = 1.
הדרך האופטימלית לחתוך לריבוע היא:
בחר 1 (מ-y) -> חיתוך אופקי עלות = 1 × מקטעים אנכיים = 1
כעת מקטעים אופקיים = 2 מקטעים אנכיים = 1.
בחר 1 (מ-y) -> חיתוך אופקי עלות = 1 × מקטעים אנכיים = 1
כעת מקטעים אופקיים = 3 מקטעים אנכיים = 1.
בחר 1 (מ-y) -> חיתוך אופקי עלות = 1 × מקטעים אנכיים = 1
כעת מקטעים אופקיים = 4 מקטעים אנכיים = 1.
בחר 1 (מ-x) -> חיתוך אנכי עלות = 1 × מקטעים אופקיים = 4
כעת מקטעים אופקיים = 4 מקטעים אנכיים = 2.
בחר 1 (מ-x) -> חיתוך אנכי עלות = 1 × מקטעים אופקיים = 4
כעת מקטעים אופקיים = 4 מקטעים אנכיים = 3.
בחר 1 (מ-x) -> חיתוך אנכי עלות = 1 × מקטעים אופקיים = 4
כעת מקטעים אופקיים = 4 מקטעים אנכיים = 4
אז העלות הכוללת = 1 + 1 + 1 + 4 + 4 + 4 = 15.

תוכן עניינים

[גישה נאיבית] נסה את כל התמורות - O((n+m)!×(n+m)) זמן ו-O(n+m) מרחב
[גישה צפויה] שימוש בטכניקה חמדנית - O( n (log n)+m (log m)) זמן ו-O(1) מרחב

[גישה נאיבית] נסה את כל התמורות - O((n+m)!×(n+m)) זמן ו-O(n+m) מרחב

הרעיון הוא ליצור את כל התמורות האפשריות של החתכים הנתונים ולאחר מכן לחשב את העלות עבור כל תמורות. לבסוף להחזיר את העלות המינימלית ביניהם.

פֶּתֶק: גישה זו אינה ריאלית עבור תשומות גדולות יותר מכיוון שמספר התמורות גדל באופן פקטוריאלי כ- (m+n-2)!.
עבור כל תמורה עלינו לחשב את העלות בזמן O(m+n). מכאן שמורכבות הזמן הכוללת הופכת ל-O((m+n−2)!×(m+n)).

[גישה צפויה] שימוש בטכניקה חמדנית - O( n (log n)+m (log m)) זמן ו-O(1) מרחב

הרעיון הוא לבצע את החתכים היקרים ביותר באמצעות א גישה חמדנית . התצפית היא שבחירה בקיצוץ העלויות הגבוה ביותר בכל שלב מפחיתה עלויות עתידיות על ידי השפעה על מספר חלקים בבת אחת. אנו ממיינים את העלויות האנכיות (x) והאופקיות (y) לפי סדר יורד ואז בוחרים באופן איטרטיבי את הגדול יותר כדי למקסם את החיסכון בעלויות. החתכים הנותרים מעובדים בנפרד כדי להבטיח שכל החלקים מפוצלים בצורה מיטבית.

מה קורה כשאנחנו עושים חתך?

חיתוך אופקי → אתה חותך לרוחב כך שמספר הרצועות האופקיות יגדל (hCount++). אבל העלות מוכפלת ב-vCount (מספר הרצועות האנכיות) מכיוון שהחתך האופקי צריך לעבור דרך כל הקטעים האנכיים.
חיתוך אנכי → אתה חותך את הגובה כך שמספר הרצועות האנכיות גדל (vCount++). אבל העלות מוכפלת ב-hCount (מספר הרצועות האופקיות) מכיוון שהחתך האנכי צריך לעבור דרך כל הקטעים האופקיים.

שלבים לפתרון הבעיה:

מיין את מערכי x וגם y בסדר יורד.
השתמש בשני מצביעים, אחד עבור x ואחד עבור y מתחיל מהערך הגדול ביותר ומתקדם לערכים קטנים יותר.
שמרו על hCount ו VCount כדי לעקוב אחר כמה פלחים כל חתך משפיע ולעדכן אותם בהתאם.
חזור על בזמן שגם ל-x וגם ל-y יש קיצוצים לא מעובדים, תמיד בוחרים בעלות הגבוהה יותר כדי למזער את ההוצאות הכוללות.
אם ל-x יש חיתוכים שנותרו לעבד אותם עם מכפיל hCount; באופן דומה מעבדים את החתכים הנותרים עם vCount.
צבור עלות כוללת בכל שלב באמצעות הנוסחה: קצץ בעלות * מספר החלקים המושפעים ומבטיח עלות מינימלית.

C++

#include   #include #include   using namespace std; int minCost(int n int m   vector<int>& x vector<int>& y) {    // Sort the cutting costs in ascending order  sort(x.begin() x.end());  sort(y.begin() y.end());   int hCount = 1 vCount = 1;   int i = x.size() - 1 j = y.size() - 1;   int totalCost = 0;  while (i >= 0 && j >= 0) {    // Choose the larger cost cut to   // minimize future costs  if (x[i] >= y[j]) {  totalCost += x[i] * hCount;   vCount++;  i--;  }   else {  totalCost += y[j] * vCount;   hCount++;  j--;  }  }  // Process remaining vertical cuts  while (i >= 0) {  totalCost += x[i] * hCount;  vCount++;  i--;  }  // Process remaining horizontal cuts  while (j >= 0) {  totalCost += y[j] * vCount;  hCount++;  j--;  }  return totalCost; } int main() {    int n = 4 m = 6;  vector<int> x = {2 1 3 1 4};  vector<int> y = {4 1 2};  cout << minCost(n m x y) << endl;  return 0; }

Java

import java.util.Arrays; class GfG {    static int minCost(int n int m   int[] x int[] y) {    // Sort the cutting costs in ascending order  Arrays.sort(x);  Arrays.sort(y);   int hCount = 1 vCount = 1;   int i = x.length - 1 j = y.length - 1;   int totalCost = 0;  while (i >= 0 && j >= 0) {    // Choose the larger cost cut to   // minimize future costs  if (x[i] >= y[j]) {  totalCost += x[i] * hCount;   vCount++;  i--;  }   else {  totalCost += y[j] * vCount;   hCount++;  j--;  }  }  // Process remaining vertical cuts  while (i >= 0) {  totalCost += x[i] * hCount;  vCount++;  i--;  }  // Process remaining horizontal cuts  while (j >= 0) {  totalCost += y[j] * vCount;  hCount++;  j--;  }  return totalCost;  }  public static void main(String[] args) {    int n = 4m = 6;  int[] x = {2 1 3 1 4};  int[] y = {4 1 2};  System.out.println(minCost(n m x y));  } }

Python

def minCost(nm x y): # Sort the cutting costs in ascending order x.sort() y.sort() hCount vCount = 1 1 i j = len(x) - 1 len(y) - 1 totalCost = 0 while i >= 0 and j >= 0: # Choose the larger cost cut to  # minimize future costs if x[i] >= y[j]: totalCost += x[i] * hCount vCount += 1 i -= 1 else: totalCost += y[j] * vCount hCount += 1 j -= 1 # Process remaining vertical cuts while i >= 0: totalCost += x[i] * hCount vCount += 1 i -= 1 # Process remaining horizontal cuts while j >= 0: totalCost += y[j] * vCount hCount += 1 j -= 1 return totalCost if __name__ == '__main__': nm = 4 6 x = [2 1 3 1 4] y = [4 1 2] print(minCost(nmx y))

using System; class GfG {  public static int minCost(int n int m   int[] x int[] y) {    // Sort the cutting costs in ascending order  Array.Sort(x);  Array.Sort(y);  int hCount = 1 vCount = 1;  int i = x.Length - 1 j = y.Length - 1;  int totalCost = 0;  // Process the cuts in greedy manner  while (i >= 0 && j >= 0) {    // Choose the larger cost cut to   // minimize future costs  if (x[i] >= y[j]) {  totalCost += x[i] * hCount;  vCount++;  i--;  }  else {  totalCost += y[j] * vCount;  hCount++;  j--;  }  }  // Process remaining vertical cuts  while (i >= 0) {  totalCost += x[i] * hCount;  vCount++;  i--;  }  // Process remaining horizontal cuts  while (j >= 0) {  totalCost += y[j] * vCount;  hCount++;  j--;  }  return totalCost;  }    public static void Main() {    int n=4m=6;  int[] x = {2 1 3 1 4};  int[] y = {4 1 2};  Console.WriteLine(minCost(nm x y));  } }

JavaScript

function minCost( nm x y) {    // Sort the cutting costs in ascending order  x.sort((a b) => a - b);  y.sort((a b) => a - b);  let hCount = 1 vCount = 1;  let i = x.length - 1 j = y.length - 1;  let totalCost = 0;  while (i >= 0 && j >= 0) {    // Choose the larger cost cut to   // minimize future costs  if (x[i] >= y[j]) {  totalCost += x[i] * hCount;  vCount++;  i--;  }   else {  totalCost += y[j] * vCount;  hCount++;  j--;  }  }  // Process remaining vertical cuts  while (i >= 0) {  totalCost += x[i] * hCount;  vCount++;  i--;  }  // Process remaining horizontal cuts  while (j >= 0) {  totalCost += y[j] * vCount;  hCount++;  j--;  }  return totalCost; } // Driver Code let n = 4m = 6; let x = [2 1 3 1 4]; let y = [4 1 2]; console.log(minCost(nm x y));

תְפוּקָה