עץ הביטוי הוא עץ המשמש לייצוג הביטויים השונים. מבנה נתוני העץ משמש לייצוג ההצהרות הביטוייות. בעץ זה, הצומת הפנימי תמיד מציין את האופרטורים.
- צמתי העלים תמיד מציינים את האופרנדים.
- הפעולות מבוצעות תמיד על אופרנדים אלה.
- המפעיל הנוכח בעומק העץ נמצא תמיד בעדיפות הגבוהה ביותר.
- המפעיל, שלא נמצא הרבה בעומק העץ, נמצא תמיד בעדיפות הנמוכה ביותר בהשוואה למפעילים השוכבים בעומק.
- האופרנד תמיד יוצג בעומק העץ; לפיכך הוא נחשב ל עדיפות עליונה בין כל המפעילים.
- בקיצור, אנחנו יכולים לסכם את זה כערך הקיים בעומק העץ נמצא בעדיפות הגבוהה ביותר בהשוואה לשאר האופרטורים הנמצאים בראש העץ.
- השימוש העיקרי בעצי הביטוי הללו הוא שהם רגילים להעריך, לנתח ו לְשַׁנוֹת הביטויים השונים.
- הוא משמש גם כדי לגלות את האסוציאטיביות של כל אופרטור בביטוי.
- לדוגמה, האופרטור + הוא האסוציאטיבי השמאלי ו-/ הוא האסוציאטיבי הימני.
- הדילמה של אסוציאטיביות זו נפתרה על ידי שימוש בעצי הביטוי.
- עצי ביטוי אלו נוצרים על ידי שימוש בדקדוק נטול הקשר.
- שיכנו כלל בדקדוקים נטולי הקשר לפני כל הפקת דקדוק.
- כללים אלו ידועים גם בתור כללים סמנטיים, ועל ידי שימוש בכללים סמנטיים אלו, נוכל בקלות לבנות את עצי הביטוי.
- זהו אחד החלקים העיקריים בתכנון המהדר ושייך לשלב הניתוח הסמנטי.
- בניתוח סמנטי זה, נשתמש בתרגומים מכווני תחביר, ובצורת פלט, נפיק את עץ הניתוח המוער.
- עץ ניתוח מוער אינו אלא הניתוח הפשוט המשויך לתכונת הסוג ולכל כלל ייצור.
- המטרה העיקרית של השימוש בעצי הביטוי היא ליצור ביטויים מורכבים וניתן להעריך אותם בקלות באמצעות עצי ביטוי אלו.
- הוא בלתי ניתן לשינוי, וברגע שיצרנו עץ ביטוי, לא נוכל לשנות אותו או לשנות אותו עוד יותר.
- כדי לבצע שינויים נוספים, נדרש לבנות את עץ הביטוי החדש במלואו.
- הוא משמש גם כדי לפתור את הערכת ביטוי postfix, קידומת ו-infix.
עצי ביטוי ממלאים תפקיד חשוב מאוד בייצוג ברמת השפה קוד בצורת הנתונים, המאוחסנים בעיקר במבנה דמוי עץ. הוא משמש גם בייצוג הזיכרון של למבדה ביטוי. באמצעות מבנה נתוני העץ, נוכל לבטא את ביטוי הלמבדה בצורה שקוף ומפורש יותר. הוא נוצר לראשונה כדי להמיר את קטע הקוד לפלח הנתונים כך שניתן להעריך את הביטוי בקלות.
עץ הביטוי הוא עץ בינארי שבו כל צומת חיצוני או עלה מתאים לאופרנד וכל צומת פנימי או אב מתאים לאופרטורים כך למשל עץ ביטוי עבור 7 + ((1+8)*3) יהיה:
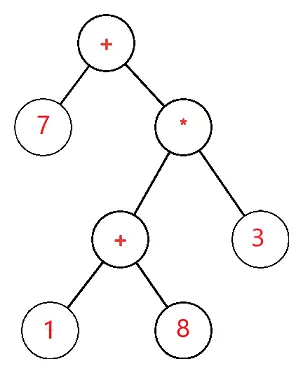
תן S להיות עץ הביטוי
אם S אינו ריק, אז
אם S.value הוא אופרנד, אז
החזר S.value
x = solve(S.left)
y = solve(S.right)
Return calculate(x, y, S.value)
כאן בדוגמה שלמעלה, עץ הביטוי השתמש בדקדוק נטול הקשר.
יש לנו כמה הפקות הקשורות לכמה כללי ייצור בדקדוק הזה, המכונה בעיקר כללים סמנטיים . אנו יכולים להגדיר את התוצאה המופקת מכללי הייצור המתאימים באמצעות כללים סמנטיים אלה. כאן השתמשנו בפרמטר הערך, שיחשב את התוצאה ויחזיר אותה לסמל ההתחלה של הדקדוק. S.left יחשב את הילד השמאלי של הצומת, ובאופן דומה, ניתן לחשב את הילד הימני של הצומת באמצעות הפרמטר S.right.
שימוש בעץ הביטוי
- המטרה העיקרית של השימוש בעצי הביטוי היא ליצור ביטויים מורכבים וניתן להעריך אותם בקלות באמצעות עצי ביטוי אלו.
- הוא משמש גם כדי לגלות את האסוציאטיביות של כל אופרטור בביטוי.
- הוא משמש גם כדי לפתור את הערכת ביטוי postfix, קידומת ו-infix.
יישום עץ ביטוי
כדי ליישם את עץ הביטוי ולכתוב את התוכנית שלו, נידרש להשתמש במבנה נתונים מחסנית.
מכיוון שאנו יודעים שהמחסנית מבוססת על עיקרון ה-LIFO האחרון נכנס ראשון החוצה, אלמנט הנתונים שנדחף לאחרונה לתוך המחסנית הופץ החוצה בכל פעם שנדרש. לצורך היישום שלה, נעשה שימוש בשתי הפעולות העיקריות של המחסנית, push ו-pop. באמצעות פעולת ה-push, נדחוף את אלמנט הנתונים לתוך המחסנית, ובאמצעות פעולת ה-pop נסיר את אלמנט הנתונים מהמחסנית.
הפונקציות העיקריות של המחסנית ביישום עץ הביטוי:
קודם כל, נערוך סריקה של הביטוי הנתון בצורה משמאל לימין, ואז אחד אחד נבדוק את התו המזוהה,
- אם תו סרוק הוא אופרנד, נחיל את פעולת הדחיפה ונדחוף אותה לערימה.
- אם תו סרוק הוא אופרטור, נפעיל את פעולת ה-pop לתוכו כדי להסיר את שני הערכים מהמחסנית כדי להפוך אותם לילד שלו, ולאחר מכן נדחוף לאחור את צומת האב הנוכחי לתוך המחסנית.
יישום עץ ביטוי בשפת תכנות C
// C program for expression tree implementation #include #include /* The below structure node is defined as a node of a binary tree consists of left child and the right child, along with the pointer next which points to the next node */ struct node { char info ; struct node* l ; struct node* r ; struct node* nxt ; }; struct node *head=NULL; /* Helper function that allocates a new node with the given data and NULL left and right pointers. */ struct node* newnode(char data) { struct node* node = (struct node*) malloc ( sizeof ( struct node ) ) ; node->info = data ; node->l = NULL ; node->r = NULL ; node->nxt = NULL ; return ( node ) ; } void Inorder(struct node* node) { if ( node == NULL) return ; else { /* first recur on left child */ Inorder ( node->l ) ; /* then print the data of node */ printf ( '%c ' , node->info ) ; /* now recur on right child */ Inorder ( node->r ) ; } } void push ( struct node* x ) { if ( head == NULL ) head = x ; else { ( x )->nxt = head ; head = x ; } // struct node* temp ; // while ( temp != NULL ) // { // printf ( ' %c ' , temp->info ) ; // temp = temp->nxt ; // } } struct node* pop() { // Poping out the top most [pointed with head] element struct node* n = head ; head = head->nxt ; return n ; } int main() { char t[] = { 'X' , 'Y' , 'Z' , '*' , '+' , 'W' , '/' } ; int n = sizeof(t) / sizeof(t[0]) ; int i ; struct node *p , *q , *s ; for ( i = 0 ; i <n ; i++ ) { if read character is operator then popping two other elements from stack and making a binary tree ( t[i]="=" '+' || '-' '*' ' '^' s="newnode" t [ i ] p="pop()" q="pop()" s->l = q ; s->r = p; push(s); } else { s = newnode ( t [ i ] ) ; push ( s ) ; } } printf ( ' The Inorder Traversal of Expression Tree: ' ) ; Inorder ( s ) ; return 0 ; } </n> הפלט של התוכנית לעיל הוא:
X + Y * Z / W
הטמעת עץ ביטוי בשפת תכנות C++
// C++ program for expression tree #include using namespace std ; /* The below class node is defined as a node of a binary tree consists of left child and the right child, along with the pointer next which points to the next node */ class node { public: char info ; node* l ; node* r ; node* nxt = NULL ; node ( char c ) { this->info = c ; l = NULL ; r = NULL ; } node() { l = NULL ; r = NULL ; } friend class Stack ; friend class tree ; } ; class Stack { node* head = NULL ; public: void push ( node* ) ; node* pop() ; friend class tree ; } ; class tree { public: void inorder ( node* x ) { // cout<<'tree in inorder traversal is: '<l ) ; cout <info <r } void stack::push( node* x { if ( head="=" null we are inserting here nodes at the top of stack [following lifo principle] else x->nxt = head ; head = x ; } } node* Stack::pop() { // Poping out the top most [ pointed with head ] element node* p = head ; head = head->nxt ; return p ; } int main() { string str = 'XYZ*+W/' ; // If you wish take input from user: //cout << 'Insert Postorder Expression: ' <> s; Stack s ; tree t ; node *p, *q, *re; int n = str.length() ; for ( int i = 0 ; i <n ; i++ ) { if ( str[ i ]="=" '+' || '-' '*' ' '^') re="new" node( str[i] p="s.pop()" q="s.pop()" re->l = q ; re->r = p ; s.push(re) ; } else { re = new node( str[ i ] ) ; s.push(re) ; } } cout << ' The Inorder Traversal of Expression Tree: ' ; t.inorder(re) ; return 0 ; } </n></'tree> הפלט של התוכנית לעיל הוא:
X + Y * Z / W
יישום עץ ביטוי בשפת תכנות ג'אווה
// Java program for expression tree import java.util.* ; /* The below class node is defined as a node of a binary tree consists of left child and the right child, along with the pointer next which points to the next node */ class Node { char info ; Node l , r ; public Node(char data) { this.info = data ; l = null ; r = null ; } } public class Main { public static boolean isOperator ( char ch ) { if ( ch == '+' || ch == '-' || ch == '*' || ch == '/' || ch == '^' ) { return true ; } return false ; } public static Node Tree ( String postfix ) { Stack st = new Stack(); Node t1,t2,temp ; for ( int i = 0 ; i <p> <strong>The output of the above program is:</strong> </p> <pre> X + Y * Z / W </pre> <hr> 