במאמר זה, נדון באלגוריתם Quicksort. גם הליך העבודה של Quicksort הוא פשוט. מאמר זה יהיה מאוד מועיל ומעניין לסטודנטים מכיוון שהם עשויים להתמודד עם מיון מהיר כשאלה בבחינות שלהם. לכן, חשוב לדון בנושא.

מיון הוא דרך לסדר פריטים בצורה שיטתית. Quicksort הוא אלגוריתם המיון הנפוץ שעושה n log n השוואות במקרה ממוצע למיון מערך של n אלמנטים. זהו אלגוריתם מיון מהיר יותר ויעיל במיוחד. אלגוריתם זה עוקב אחר גישת ההפרד ומשול. הפרד וכבש היא טכניקה של פירוק האלגוריתמים לתת-בעיות, ואז פתרון בעיות המשנה, ושילוב התוצאות יחד כדי לפתור את הבעיה המקורית.

אלגוריתם kmp

לחלק: בחלוקה, תחילה בחר אלמנט ציר. לאחר מכן, חלקו או סדרו מחדש את המערך לשני תת-מערכים כך שכל אלמנט בתת-מערך השמאלי קטן או שווה לאלמנט pivot וכל אלמנט בתת-מערך הימני גדול יותר מאלמנט pivot.

לִכבּוֹשׁ: באופן רקורסיבי, מיין שני מערכי משנה עם Quicksort.

לְשַׁלֵב: שלב את המערך שכבר ממוין.

Quicksort בוחר אלמנט בתור ציר, ואז הוא מחלק את המערך הנתון סביב אלמנט הציר שנבחר. במיון מהיר, מערך גדול מחולק לשני מערכים שבהם אחד מחזיק ערכים קטנים מהערך שצוין (Pivot), ומערך אחר מחזיק את הערכים הגדולים מהציר.

לאחר מכן, מערכי משנה משמאל וימין מחולקים גם הם באמצעות אותה גישה. זה ימשיך עד שהאלמנט הבודד יישאר במערך המשנה.

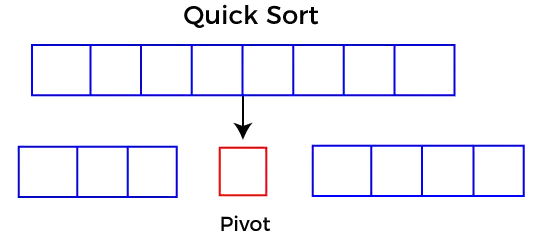
בחירת הציר

בחירת ציר טוב היא הכרחית ליישום מהיר של quicksort. עם זאת, אופייני לקבוע ציר טוב. כמה מהדרכים לבחירת ציר הן כדלקמן -

• Pivot יכול להיות אקראי, כלומר בחר את הציר האקראי מהמערך הנתון.
• Pivot יכול להיות האלמנט הימני ביותר של האלמנט השמאלי ביותר של המערך הנתון.
• בחר חציון כאלמנט הציר.

אַלגוֹרִיתְם

אַלגוֹרִיתְם:

 QUICKSORT (array A, start, end) { 1 if (start <end) 2 3 4 5 6 { p="partition(A," start, end) quicksort (a, - 1) + 1, } < pre> <p> <strong>Partition Algorithm:</strong> </p> <p>The partition algorithm rearranges the sub-arrays in a place.</p> <pre> PARTITION (array A, start, end) { 1 pivot ? A[end] 2 i ? start-1 3 for j ? start to end -1 { 4 do if (A[j] <pivot) 1 5 6 7 8 9 { then i ? + swap a[i] with a[j] }} a[i+1] a[end] return i+1 } < pre> <h2>Working of Quick Sort Algorithm</h2> <p>Now, let&apos;s see the working of the Quicksort Algorithm.</p> <p>To understand the working of quick sort, let&apos;s take an unsorted array. It will make the concept more clear and understandable.</p> <p>Let the elements of array are -</p> <img src="//techcodeview.com/img/ds-tutorial/75/quick-sort-algorithm-2.webp" alt="Quick Sort Algorithm"> <p>In the given array, we consider the leftmost element as pivot. So, in this case, a[left] = 24, a[right] = 27 and a[pivot] = 24.</p> <p>Since, pivot is at left, so algorithm starts from right and move towards left.</p> <img src="//techcodeview.com/img/ds-tutorial/75/quick-sort-algorithm-3.webp" alt="Quick Sort Algorithm"> <p>Now, a[pivot] <a[right], so algorithm moves forward one position towards left, i.e. -< p> <img src="//techcodeview.com/img/ds-tutorial/75/quick-sort-algorithm-4.webp" alt="Quick Sort Algorithm"> <p>Now, a[left] = 24, a[right] = 19, and a[pivot] = 24.</p> <p>Because, a[pivot] &gt; a[right], so, algorithm will swap a[pivot] with a[right], and pivot moves to right, as -</p> <img src="//techcodeview.com/img/ds-tutorial/75/quick-sort-algorithm-5.webp" alt="Quick Sort Algorithm"> <p>Now, a[left] = 19, a[right] = 24, and a[pivot] = 24. Since, pivot is at right, so algorithm starts from left and moves to right.</p> <p>As a[pivot] &gt; a[left], so algorithm moves one position to right as -</p> <img src="//techcodeview.com/img/ds-tutorial/75/quick-sort-algorithm-6.webp" alt="Quick Sort Algorithm"> <p>Now, a[left] = 9, a[right] = 24, and a[pivot] = 24. As a[pivot] &gt; a[left], so algorithm moves one position to right as -</p> <img src="//techcodeview.com/img/ds-tutorial/75/quick-sort-algorithm-7.webp" alt="Quick Sort Algorithm"> <p>Now, a[left] = 29, a[right] = 24, and a[pivot] = 24. As a[pivot] <a[left], so, swap a[pivot] and a[left], now pivot is at left, i.e. -< p> <img src="//techcodeview.com/img/ds-tutorial/75/quick-sort-algorithm-8.webp" alt="Quick Sort Algorithm"> <p>Since, pivot is at left, so algorithm starts from right, and move to left. Now, a[left] = 24, a[right] = 29, and a[pivot] = 24. As a[pivot] <a[right], so algorithm moves one position to left, as -< p> <img src="//techcodeview.com/img/ds-tutorial/75/quick-sort-algorithm-9.webp" alt="Quick Sort Algorithm"> <p>Now, a[pivot] = 24, a[left] = 24, and a[right] = 14. As a[pivot] &gt; a[right], so, swap a[pivot] and a[right], now pivot is at right, i.e. -</p> <img src="//techcodeview.com/img/ds-tutorial/75/quick-sort-algorithm-10.webp" alt="Quick Sort Algorithm"> <p>Now, a[pivot] = 24, a[left] = 14, and a[right] = 24. Pivot is at right, so the algorithm starts from left and move to right.</p> <img src="//techcodeview.com/img/ds-tutorial/75/quick-sort-algorithm-11.webp" alt="Quick Sort Algorithm"> <p>Now, a[pivot] = 24, a[left] = 24, and a[right] = 24. So, pivot, left and right are pointing the same element. It represents the termination of procedure.</p> <p>Element 24, which is the pivot element is placed at its exact position.</p> <p>Elements that are right side of element 24 are greater than it, and the elements that are left side of element 24 are smaller than it.</p> <img src="//techcodeview.com/img/ds-tutorial/75/quick-sort-algorithm-12.webp" alt="Quick Sort Algorithm"> <p>Now, in a similar manner, quick sort algorithm is separately applied to the left and right sub-arrays. After sorting gets done, the array will be -</p> <img src="//techcodeview.com/img/ds-tutorial/75/quick-sort-algorithm-13.webp" alt="Quick Sort Algorithm"> <h2>Quicksort complexity</h2> <p>Now, let&apos;s see the time complexity of quicksort in best case, average case, and in worst case. We will also see the space complexity of quicksort.</p> <h3>1. Time Complexity</h3> <table class="table"> <tr> <th>Case</th> <th>Time Complexity</th> </tr> <tr> <td> <strong>Best Case</strong> </td> <td>O(n*logn)</td> </tr> <tr> <td> <strong>Average Case</strong> </td> <td>O(n*logn)</td> </tr> <tr> <td> <strong>Worst Case</strong> </td> <td>O(n<sup>2</sup>)</td> </tr> </table> <ul> <tr><td>Best Case Complexity -</td> In Quicksort, the best-case occurs when the pivot element is the middle element or near to the middle element. The best-case time complexity of quicksort is <strong>O(n*logn)</strong> . </tr><tr><td>Average Case Complexity -</td> It occurs when the array elements are in jumbled order that is not properly ascending and not properly descending. The average case time complexity of quicksort is <strong>O(n*logn)</strong> . </tr><tr><td>Worst Case Complexity -</td> In quick sort, worst case occurs when the pivot element is either greatest or smallest element. Suppose, if the pivot element is always the last element of the array, the worst case would occur when the given array is sorted already in ascending or descending order. The worst-case time complexity of quicksort is <strong>O(n<sup>2</sup>)</strong> . </tr></ul> <p>Though the worst-case complexity of quicksort is more than other sorting algorithms such as <strong>Merge sort</strong> and <strong>Heap sort</strong> , still it is faster in practice. Worst case in quick sort rarely occurs because by changing the choice of pivot, it can be implemented in different ways. Worst case in quicksort can be avoided by choosing the right pivot element.</p> <h3>2. Space Complexity</h3> <table class="table"> <tr> <td> <strong>Space Complexity</strong> </td> <td>O(n*logn)</td> </tr> <tr> <td> <strong>Stable</strong> </td> <td>NO</td> </tr> </table> <ul> <li>The space complexity of quicksort is O(n*logn).</li> </ul> <h2>Implementation of quicksort</h2> <p>Now, let&apos;s see the programs of quicksort in different programming languages.</p> <p> <strong>Program:</strong> Write a program to implement quicksort in C language.</p> <pre> #include /* function that consider last element as pivot, place the pivot at its exact position, and place smaller elements to left of pivot and greater elements to right of pivot. */ int partition (int a[], int start, int end) { int pivot = a[end]; // pivot element int i = (start - 1); for (int j = start; j <= 27 end - 1; j++) { if current element is smaller than the pivot (a[j] < pivot) i++; increment index of int t="a[i];" a[i]="a[j];" a[j]="t;" } a[i+1]="a[end];" a[end]="t;" return (i + 1); * function to implement quick sort void quick(int a[], start, end) a[]="array" be sorted, start="Starting" index, (start p="partition(a," end); partitioning quick(a, 1, print an array printarr(int n) i; for i n; i++) printf('%d ', a[i]); main() 24, 9, 29, 14, 19, }; n="sizeof(a)" sizeof(a[0]); printf('before sorting elements are 
'); printarr(a, n); 0, printf('
after 0; pre> <p> <strong>Output:</strong> </p> <img src="//techcodeview.com/img/ds-tutorial/75/quick-sort-algorithm-14.webp" alt="Quick Sort Algorithm"> <p> <strong>Program:</strong> Write a program to implement quick sort in C++ language.</p> <pre> #include using namespace std; /* function that consider last element as pivot, place the pivot at its exact position, and place smaller elements to left of pivot and greater elements to right of pivot. */ int partition (int a[], int start, int end) { int pivot = a[end]; // pivot element int i = (start - 1); for (int j = start; j <= 26 end - 1; j++) { if current element is smaller than the pivot (a[j] < pivot) i++; increment index of int t="a[i];" a[i]="a[j];" a[j]="t;" } a[i+1]="a[end];" a[end]="t;" return (i + 1); * function to implement quick sort void quick(int a[], start, end) a[]="array" be sorted, start="Starting" index, (start p="partition(a," end); partitioning quick(a, 1, print an array printarr(int n) i; for i n; i++) cout< <a[i]<< ' '; main() 23, 8, 28, 13, 18, }; n="sizeof(a)" sizeof(a[0]); cout<<'before sorting elements are 
'; printarr(a, n); 0, cout<<'
after 0; pre> <p> <strong>Output:</strong> </p> <img src="//techcodeview.com/img/ds-tutorial/75/quick-sort-algorithm-15.webp" alt="Quick Sort Algorithm"> <p> <strong>Program:</strong> Write a program to implement quicksort in python.</p> <pre> #function that consider last element as pivot, #place the pivot at its exact position, and place #smaller elements to left of pivot and greater #elements to right of pivot. def partition (a, start, end): i = (start - 1) pivot = a[end] # pivot element for j in range(start, end): # If current element is smaller than or equal to the pivot if (a[j] <= 1 pivot): i="i" + a[i], a[j]="a[j]," a[i] a[i+1], a[end]="a[end]," a[i+1] return (i 1) # function to implement quick sort def quick(a, start, end): a[]="array" be sorted, start="Starting" index, end="Ending" index if (start < p="partition(a," end) is partitioning - 1, printarr(a): print the array for in range(len(a)): (a[i], ) a="[68," 13, 49, 58] print('before sorting elements are ') printarr(a) 0, len(a)-1) print('
after pre> <p> <strong>Output:</strong> </p> <img src="//techcodeview.com/img/ds-tutorial/75/quick-sort-algorithm-16.webp" alt="Quick Sort Algorithm"> <p> <strong>Program:</strong> Write a program to implement quicksort in Java.</p> <pre> public class Quick { /* function that consider last element as pivot, place the pivot at its exact position, and place smaller elements to left of pivot and greater elements to right of pivot. */ int partition (int a[], int start, int end) { int pivot = a[end]; // pivot element int i = (start - 1); for (int j = start; j <= 25 end - 1; j++) { if current element is smaller than the pivot (a[j] < pivot) i++; increment index of int t="a[i];" a[i]="a[j];" a[j]="t;" } a[i+1]="a[end];" a[end]="t;" return (i + 1); * function to implement quick sort void quick(int a[], start, end) a[]="array" be sorted, start="Starting" index, (start p="partition(a," end); partitioning quick(a, 1, print an array printarr(int n) i; for i n; i++) system.out.print(a[i] ' '); public static main(string[] args) 13, 18, 27, 2, 19, }; n="a.length;" system.out.println('
before sorting elements are q1="new" quick(); q1.printarr(a, n); q1.quick(a, 0, system.out.println('
after system.out.println(); pre> <p> <strong>Output</strong> </p> <p>After the execution of above code, the output will be -</p> <img src="//techcodeview.com/img/ds-tutorial/75/quick-sort-algorithm-17.webp" alt="Quick Sort Algorithm"> <p> <strong>Program:</strong> Write a program to implement quick sort in php.</p> <pre> <?php /* function that consider last element as pivot, place the pivot at its exact position, and place smaller elements to left of pivot and greater elements to right of pivot. */ function partition (&$a, $start, $end) { $pivot = $a[$end]; // pivot element $i = ($start - 1); for ($j = $start; $j <= $end - 1; $j++) { // If current element is smaller than the pivot if ($a[$j] < $pivot) { $i++; // increment index of smaller element $t = $a[$i]; $a[$i] = $a[$j]; $a[$j] = $t; } } $t = $a[$i+1]; $a[$i+1] = $a[$end]; $a[$end] = $t; return ($i + 1); } /* function to implement quick sort */ function quick(&$a, $start, $end) /* a[] = array to be sorted, start = Starting index, end = Ending index */ { if ($start < $end) { $p = partition($a, $start, $end); //p is partitioning index quick($a, $start, $p - 1); quick($a, $p + 1, $end); } } function printArray($a, $n) { for($i = 0; $i < $n; $i++) { print_r($a[$i]); echo ' '; } } $a = array( 89, 47, 2, 17, 8, 19 ); $n = count($a); echo 'Before sorting array elements are - <br>&apos;; printArray($a, $n); quick($a, 0, $n - 1); echo &apos; <br> After sorting array elements are - <br>&apos;; printArray($a, $n); ?&gt; </pre> <p> <strong>Output</strong> </p> <p>After the execution of above code, the output will be -</p> <img src="//techcodeview.com/img/ds-tutorial/75/quick-sort-algorithm-18.webp" alt="Quick Sort Algorithm"> <p>So, that&apos;s all about the article. Hope the article will be helpful and informative to you.</p> <p>This article was not only limited to the algorithm. Along with the algorithm, we have also discussed the quick sort complexity, working, and implementation in different programming languages.</p> <hr></=></pre></=></pre></=></pre></=></pre></a[right],></p></a[left],></p></a[right],></p></pivot)></pre></end)>

תְפוּקָה

לאחר ביצוע הקוד לעיל, הפלט יהיה -

אז, זה הכל לגבי המאמר. מקווה שהמאמר יהיה מועיל ואינפורמטיבי עבורך.

מאמר זה לא היה מוגבל רק לאלגוריתם. יחד עם האלגוריתם, דנו גם במורכבות המיון המהיר, העבודה והיישום בשפות תכנות שונות.

המרת מחרוזת ל-int