- DFA מתייחס לאוטומטים סופיים דטרמיניסטיים. דטרמיניסטי מתייחס לייחודיות של החישוב. האוטומטים הסופיים נקראים אוטומטים סופיים דטרמיניסטיים אם המכונה נקראת מחרוזת קלט סמל אחד בכל פעם.
- ב-DFA, יש רק נתיב אחד לקלט ספציפי מהמצב הנוכחי למצב הבא.
- DFA אינו מקבל את המהלך האפס, כלומר, ה-DFA אינו יכול לשנות מצב ללא תו קלט כלשהו.
- DFA יכול להכיל מספר מצבים סופיים. הוא משמש בניתוח לקסיקלי בקומפיילר.
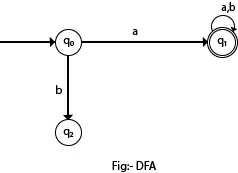
בתרשים הבא, אנו יכולים לראות שממצב q0 עבור קלט a, יש רק נתיב אחד שהולך ל-q1. באופן דומה, מ-q0, יש רק נתיב אחד לקלט b שעובר ל-q2.
הגדרה רשמית של DFA
DFA הוא אוסף של 5-tuples כמו שתיארנו בהגדרה של FA.
Q: finite set of states ∑: finite set of the input symbol q0: initial state F: final state δ: Transition function
ניתן להגדיר את פונקציית המעבר כ:
δ: Q x ∑→Q
ייצוג גרפי של DFA
DFA יכול להיות מיוצג על ידי דיגרפים הנקראים דיאגרמת מצב. שבו:
- המדינה מיוצגת על ידי קודקודים.
- הקשת המסומנת בתו קלט מציגה את המעברים.
- המצב ההתחלתי מסומן בחץ.
- המצב הסופי מסומן במעגל כפול.
דוגמה 1:
Q = {q0, q1, q2} ∑ = {0, 1} q0 = {q0} F = {q2} פִּתָרוֹן:
תרשים מעבר:

טבלת מעבר:
| מצב נוכחי | המצב הבא עבור קלט 0 | מצב הקלט הבא 1 |
|---|---|---|
| →q0 | q0 | ש1 |
| ש1 | ש2 | ש1 |
| *q2 | ש2 | ש2 |
דוגמה 2:
DFA עם ∑ = {0, 1} מקבל הכל מתחיל ב-0.
פִּתָרוֹן:

הֶסבֵּר:
- בתרשים שלמעלה, אנו יכולים לראות שב-0 נתון כקלט ל-DFA במצב q0, ה-DFA משנה את המצב ל-q1 ותמיד עובר למצב סופי q1 בכניסה מתחילה 0. הוא יכול לקבל 00, 01, 000, 001... .וכו. הוא לא יכול לקבל שום מחרוזת שמתחילה ב-1, כי היא לעולם לא תעבור למצב סופי במחרוזת שמתחילה ב-1.
דוגמה 3:
DFA עם ∑ = {0, 1} מקבל את כל המסתיימות ב-0.
פִּתָרוֹן:

הֶסבֵּר:
בתרשים לעיל, אנו יכולים לראות שבנתון 0 כקלט ל-DFA במצב q0, ה-DFA משנה מצב ל-q1. זה יכול לקבל כל מחרוזת שמסתיימת ב-0 כמו 00, 10, 110, 100... וכו'. זה לא יכול לקבל שום מחרוזת שמסתיימת ב-1, כי היא לעולם לא תעבור למצב הסופי q1 בקלט 1, כך שהמחרוזת המסתיימת ב-1, לא תתקבל או תידחה.
