תנאי מוקדם - עץ פניוויק
אנו יודעים שכדי לענות על שאילתות סכום טווח על מערך 1-D בעץ בינארי בינארי ביעילות (או עץ Fenwick) הוא הבחירה הטובה ביותר (אפילו טובה יותר מעץ הקטע בגלל פחות דרישות זיכרון ומעט מהירות יותר מעץ הקטע).
האם אנו יכולים לענות על שאילתות סכום תת-מטריקס ביעילות באמצעות עץ אינדקס בינארי?
התשובה היא כֵּן ו זה אפשרי באמצעות א ביט 2D שזה לא אלא מערך של 1D.
jframe
אַלגוֹרִיתְם:
אנו שוקלים את הדוגמה שלהלן. נניח שעלינו למצוא את סכום כל המספרים באזור המודגש:
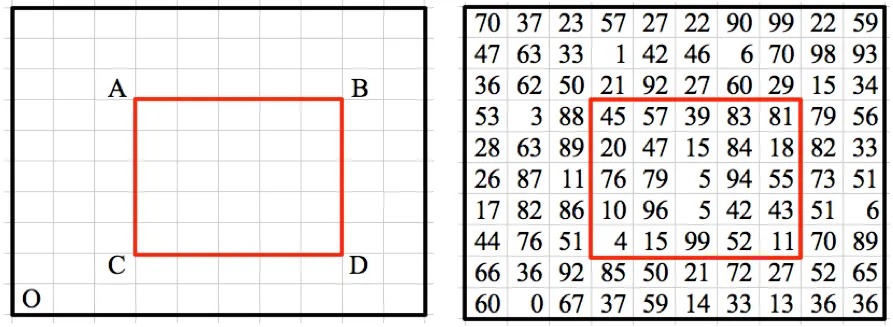
אנו מניחים את מקור המטריצה בתחתית - O. ואז סיביות דו -מימדית מנצלת את העובדה
localdate java
Sum under the marked area = Sum(OB) - Sum(OD) - Sum(OA) + Sum(OC) 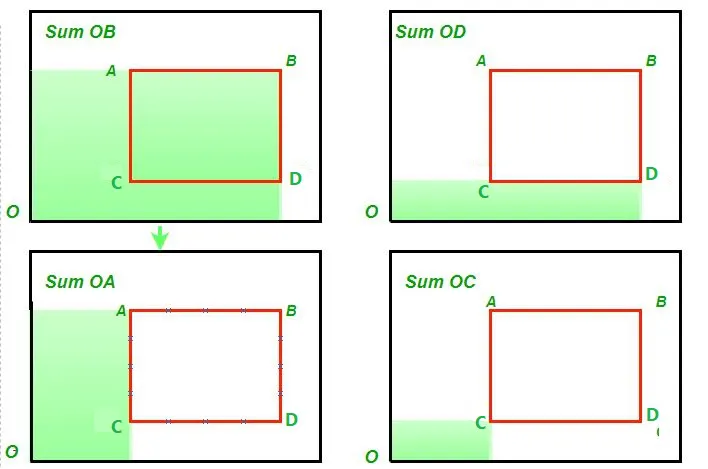
בתוכנית שלנו אנו משתמשים בפונקציה getSum (x y) שמוצאת את סכום המטריצה מ- (0 0) ל- (x y).
מכאן הנוסחה להלן:
Sum under the marked area = Sum(OB) - Sum(OD) - Sum(OA) + Sum(OC) The above formula gets reduced to Query(x1y1x2y2) = getSum(x2 y2) - getSum(x2 y1-1) - getSum(x1-1 y2) + getSum(x1-1 y1-1) אֵיפֹה
x1 y1 = X ו- Y קואורדינטות של C
x2 y2 = X ו- Y קואורדינטות של B
פונקציית updatebit (x y val) מעדכנת את כל האלמנטים שמתחת לאזור - (x y) עד (n m) היכן
נ = קואורדינטה מקסימאלית x של המטריצה כולה.
מ ' = קואורדינטות מקסימום y של המטריצה כולה.
נוהל המנוחה דומה למדי לזה של עץ צמוד בינארי 1D.
להלן יישום C ++ של עץ צמוד דו מימדי
C++/* C++ program to implement 2D Binary Indexed Tree 2D BIT is basically a BIT where each element is another BIT. Updating by adding v on (x y) means it's effect will be found throughout the rectangle [(x y) (max_x max_y)] and query for (x y) gives you the result of the rectangle [(0 0) (x y)] assuming the total rectangle is [(0 0) (max_x max_y)]. So when you query and update on this BITyou have to be careful about how many times you are subtracting a rectangle and adding it. Simple set union formula works here. So if you want to get the result of a specific rectangle [(x1 y1) (x2 y2)] the following steps are necessary: Query(x1y1x2y2) = getSum(x2 y2)-getSum(x2 y1-1) - getSum(x1-1 y2)+getSum(x1-1 y1-1) Here 'Query(x1y1x2y2)' means the sum of elements enclosed in the rectangle with bottom-left corner's co-ordinates (x1 y1) and top-right corner's co-ordinates - (x2 y2) Constraints -> x1<=x2 and y1<=y2 / y | | --------(x2y2) | | | | | | | | | | --------- | (x1y1) | |___________________________ (0 0) x--> In this program we have assumed a square matrix. The program can be easily extended to a rectangular one. */ #include
/* Java program to implement 2D Binary Indexed Tree 2D BIT is basically a BIT where each element is another BIT. Updating by adding v on (x y) means it's effect will be found throughout the rectangle [(x y) (max_x max_y)] and query for (x y) gives you the result of the rectangle [(0 0) (x y)] assuming the total rectangle is [(0 0) (max_x max_y)]. So when you query and update on this BITyou have to be careful about how many times you are subtracting a rectangle and adding it. Simple set union formula works here. So if you want to get the result of a specific rectangle [(x1 y1) (x2 y2)] the following steps are necessary: Query(x1y1x2y2) = getSum(x2 y2)-getSum(x2 y1-1) - getSum(x1-1 y2)+getSum(x1-1 y1-1) Here 'Query(x1y1x2y2)' means the sum of elements enclosed in the rectangle with bottom-left corner's co-ordinates (x1 y1) and top-right corner's co-ordinates - (x2 y2) Constraints -> x1<=x2 and y1<=y2 / y | | --------(x2y2) | | | | | | | | | | --------- | (x1y1) | |___________________________ (0 0) x--> In this program we have assumed a square matrix. The program can be easily extended to a rectangular one. */ class GFG { static final int N = 4; // N-.max_x and max_y // A structure to hold the queries static class Query { int x1 y1; // x and y co-ordinates of bottom left int x2 y2; // x and y co-ordinates of top right public Query(int x1 int y1 int x2 int y2) { this.x1 = x1; this.y1 = y1; this.x2 = x2; this.y2 = y2; } }; // A function to update the 2D BIT static void updateBIT(int BIT[][] int x int y int val) { for (; x <= N; x += (x & -x)) { // This loop update all the 1D BIT inside the // array of 1D BIT = BIT[x] for (; y <= N; y += (y & -y)) BIT[x][y] += val; } return; } // A function to get sum from (0 0) to (x y) static int getSum(int BIT[][] int x int y) { int sum = 0; for(; x > 0; x -= x&-x) { // This loop sum through all the 1D BIT // inside the array of 1D BIT = BIT[x] for(; y > 0; y -= y&-y) { sum += BIT[x][y]; } } return sum; } // A function to create an auxiliary matrix // from the given input matrix static void constructAux(int mat[][] int aux[][]) { // Initialise Auxiliary array to 0 for (int i = 0; i <= N; i++) for (int j = 0; j <= N; j++) aux[i][j] = 0; // Construct the Auxiliary Matrix for (int j = 1; j <= N; j++) for (int i = 1; i <= N; i++) aux[i][j] = mat[N - j][i - 1]; return; } // A function to construct a 2D BIT static void construct2DBIT(int mat[][] int BIT[][]) { // Create an auxiliary matrix int [][]aux = new int[N + 1][N + 1]; constructAux(mat aux); // Initialise the BIT to 0 for (int i = 1; i <= N; i++) for (int j = 1; j <= N; j++) BIT[i][j] = 0; for (int j = 1; j <= N; j++) { for (int i = 1; i <= N; i++) { // Creating a 2D-BIT using update function // everytime we/ encounter a value in the // input 2D-array int v1 = getSum(BIT i j); int v2 = getSum(BIT i j - 1); int v3 = getSum(BIT i - 1 j - 1); int v4 = getSum(BIT i - 1 j); // Assigning a value to a particular element // of 2D BIT updateBIT(BIT i j aux[i][j] - (v1 - v2 - v4 + v3)); } } return; } // A function to answer the queries static void answerQueries(Query q[] int m int BIT[][]) { for (int i = 0; i < m; i++) { int x1 = q[i].x1 + 1; int y1 = q[i].y1 + 1; int x2 = q[i].x2 + 1; int y2 = q[i].y2 + 1; int ans = getSum(BIT x2 y2) - getSum(BIT x2 y1 - 1) - getSum(BIT x1 - 1 y2) + getSum(BIT x1 - 1 y1 - 1); System.out.printf('Query(%d %d %d %d) = %dn' q[i].x1 q[i].y1 q[i].x2 q[i].y2 ans); } return; } // Driver Code public static void main(String[] args) { int mat[][] = { {1 2 3 4} {5 3 8 1} {4 6 7 5} {2 4 8 9} }; // Create a 2D Binary Indexed Tree int [][]BIT = new int[N + 1][N + 1]; construct2DBIT(mat BIT); /* Queries of the form - x1 y1 x2 y2 For example the query- {1 1 3 2} means the sub-matrix- y / 3 | 1 2 3 4 Sub-matrix 2 | 5 3 8 1 {1132} --. 3 8 1 1 | 4 6 7 5 6 7 5 0 | 2 4 8 9 | --|------ 0 1 2 3 ---. x | Hence sum of the sub-matrix = 3+8+1+6+7+5 = 30 */ Query q[] = {new Query(1 1 3 2) new Query(2 3 3 3) new Query(1 1 1 1)}; int m = q.length; answerQueries(q m BIT); } } // This code is contributed by 29AjayKumar
'''Python3 program to implement 2D Binary Indexed Tree 2D BIT is basically a BIT where each element is another BIT. Updating by adding v on (x y) means it's effect will be found throughout the rectangle [(x y) (max_x max_y)] and query for (x y) gives you the result of the rectangle [(0 0) (x y)] assuming the total rectangle is [(0 0) (max_x max_y)]. So when you query and update on this BITyou have to be careful about how many times you are subtracting a rectangle and adding it. Simple set union formula works here. So if you want to get the result of a specific rectangle [(x1 y1) (x2 y2)] the following steps are necessary: Query(x1y1x2y2) = getSum(x2 y2)-getSum(x2 y1-1) - getSum(x1-1 y2)+getSum(x1-1 y1-1) Here 'Query(x1y1x2y2)' means the sum of elements enclosed in the rectangle with bottom-left corner's co-ordinates (x1 y1) and top-right corner's co-ordinates - (x2 y2) Constraints -> x1<=x2 and y1<=y2 / y | | --------(x2y2) | | | | | | | | | | --------- | (x1y1) | |___________________________ (0 0) x--> In this program we have assumed a square matrix. The program can be easily extended to a rectangular one. ''' N = 4 # N-.max_x and max_y # A structure to hold the queries class Query: def __init__(self x1y1x2y2): self.x1 = x1; self.y1 = y1; self.x2 = x2; self.y2 = y2; # A function to update the 2D BIT def updateBIT(BITxyval): while x <= N: # This loop update all the 1D BIT inside the # array of 1D BIT = BIT[x] while y <= N: BIT[x][y] += val; y += (y & -y) x += (x & -x) return; # A function to get sum from (0 0) to (x y) def getSum(BITxy): sum = 0; while x > 0: # This loop sum through all the 1D BIT # inside the array of 1D BIT = BIT[x] while y > 0: sum += BIT[x][y]; y -= y&-y x -= x&-x return sum; # A function to create an auxiliary matrix # from the given input matrix def constructAux(mataux): # Initialise Auxiliary array to 0 for i in range(N + 1): for j in range(N + 1): aux[i][j] = 0 # Construct the Auxiliary Matrix for j in range(1 N + 1): for i in range(1 N + 1): aux[i][j] = mat[N - j][i - 1]; return # A function to construct a 2D BIT def construct2DBIT(matBIT): # Create an auxiliary matrix aux = [None for i in range(N + 1)] for i in range(N + 1) : aux[i]= [None for i in range(N + 1)] constructAux(mat aux) # Initialise the BIT to 0 for i in range(1 N + 1): for j in range(1 N + 1): BIT[i][j] = 0; for j in range(1 N + 1): for i in range(1 N + 1): # Creating a 2D-BIT using update function # everytime we/ encounter a value in the # input 2D-array v1 = getSum(BIT i j); v2 = getSum(BIT i j - 1); v3 = getSum(BIT i - 1 j - 1); v4 = getSum(BIT i - 1 j); # Assigning a value to a particular element # of 2D BIT updateBIT(BIT i j aux[i][j] - (v1 - v2 - v4 + v3)); return; # A function to answer the queries def answerQueries(qmBIT): for i in range(m): x1 = q[i].x1 + 1; y1 = q[i].y1 + 1; x2 = q[i].x2 + 1; y2 = q[i].y2 + 1; ans = getSum(BIT x2 y2) - getSum(BIT x2 y1 - 1) - getSum(BIT x1 - 1 y2) + getSum(BIT x1 - 1 y1 - 1); print('Query (' q[i].x1 ' ' q[i].y1 ' ' q[i].x2 ' ' q[i].y2 ') = ' ans sep = '') return; # Driver Code mat= [[1 2 3 4] [5 3 8 1] [4 6 7 5] [2 4 8 9]]; # Create a 2D Binary Indexed Tree BIT = [None for i in range(N + 1)] for i in range(N + 1): BIT[i]= [None for i in range(N + 1)] for j in range(N + 1): BIT[i][j]=0 construct2DBIT(mat BIT); ''' Queries of the form - x1 y1 x2 y2 For example the query- {1 1 3 2} means the sub-matrix- y / 3 | 1 2 3 4 Sub-matrix 2 | 5 3 8 1 {1132} --. 3 8 1 1 | 4 6 7 5 6 7 5 0 | 2 4 8 9 | --|------ 0 1 2 3 ---. x | Hence sum of the sub-matrix = 3+8+1+6+7+5 = 30 ''' q = [Query(1 1 3 2) Query(2 3 3 3) Query(1 1 1 1)]; m = len(q) answerQueries(q m BIT); # This code is contributed by phasing17
/* C# program to implement 2D Binary Indexed Tree 2D BIT is basically a BIT where each element is another BIT. Updating by.Adding v on (x y) means it's effect will be found throughout the rectangle [(x y) (max_x max_y)] and query for (x y) gives you the result of the rectangle [(0 0) (x y)] assuming the total rectangle is [(0 0) (max_x max_y)]. So when you query and update on this BITyou have to be careful about how many times you are subtracting a rectangle and.Adding it. Simple set union formula works here. So if you want to get the result of a specific rectangle [(x1 y1) (x2 y2)] the following steps are necessary: Query(x1y1x2y2) = getSum(x2 y2)-getSum(x2 y1-1) - getSum(x1-1 y2)+getSum(x1-1 y1-1) Here 'Query(x1y1x2y2)' means the sum of elements enclosed in the rectangle with bottom-left corner's co-ordinates (x1 y1) and top-right corner's co-ordinates - (x2 y2) Constraints -> x1<=x2 and y1<=y2 / y | | --------(x2y2) | | | | | | | | | | --------- | (x1y1) | |___________________________ (0 0) x--> In this program we have assumed a square matrix. The program can be easily extended to a rectangular one. */ using System; class GFG { static readonly int N = 4; // N-.max_x and max_y // A structure to hold the queries public class Query { public int x1 y1; // x and y co-ordinates of bottom left public int x2 y2; // x and y co-ordinates of top right public Query(int x1 int y1 int x2 int y2) { this.x1 = x1; this.y1 = y1; this.x2 = x2; this.y2 = y2; } }; // A function to update the 2D BIT static void updateBIT(int []BIT int x int y int val) { for (; x <= N; x += (x & -x)) { // This loop update all the 1D BIT inside the // array of 1D BIT = BIT[x] for (; y <= N; y += (y & -y)) BIT[xy] += val; } return; } // A function to get sum from (0 0) to (x y) static int getSum(int []BIT int x int y) { int sum = 0; for(; x > 0; x -= x&-x) { // This loop sum through all the 1D BIT // inside the array of 1D BIT = BIT[x] for(; y > 0; y -= y&-y) { sum += BIT[x y]; } } return sum; } // A function to create an auxiliary matrix // from the given input matrix static void constructAux(int []mat int []aux) { // Initialise Auxiliary array to 0 for (int i = 0; i <= N; i++) for (int j = 0; j <= N; j++) aux[i j] = 0; // Construct the Auxiliary Matrix for (int j = 1; j <= N; j++) for (int i = 1; i <= N; i++) aux[i j] = mat[N - j i - 1]; return; } // A function to construct a 2D BIT static void construct2DBIT(int []mat int []BIT) { // Create an auxiliary matrix int []aux = new int[N + 1 N + 1]; constructAux(mat aux); // Initialise the BIT to 0 for (int i = 1; i <= N; i++) for (int j = 1; j <= N; j++) BIT[i j] = 0; for (int j = 1; j <= N; j++) { for (int i = 1; i <= N; i++) { // Creating a 2D-BIT using update function // everytime we/ encounter a value in the // input 2D-array int v1 = getSum(BIT i j); int v2 = getSum(BIT i j - 1); int v3 = getSum(BIT i - 1 j - 1); int v4 = getSum(BIT i - 1 j); // Assigning a value to a particular element // of 2D BIT updateBIT(BIT i j aux[ij] - (v1 - v2 - v4 + v3)); } } return; } // A function to answer the queries static void answerQueries(Query []q int m int []BIT) { for (int i = 0; i < m; i++) { int x1 = q[i].x1 + 1; int y1 = q[i].y1 + 1; int x2 = q[i].x2 + 1; int y2 = q[i].y2 + 1; int ans = getSum(BIT x2 y2) - getSum(BIT x2 y1 - 1) - getSum(BIT x1 - 1 y2) + getSum(BIT x1 - 1 y1 - 1); Console.Write('Query({0} {1} {2} {3}) = {4}n' q[i].x1 q[i].y1 q[i].x2 q[i].y2 ans); } return; } // Driver Code public static void Main(String[] args) { int []mat = { {1 2 3 4} {5 3 8 1} {4 6 7 5} {2 4 8 9} }; // Create a 2D Binary Indexed Tree int []BIT = new int[N + 1N + 1]; construct2DBIT(mat BIT); /* Queries of the form - x1 y1 x2 y2 For example the query- {1 1 3 2} means the sub-matrix- y / 3 | 1 2 3 4 Sub-matrix 2 | 5 3 8 1 {1132} --. 3 8 1 1 | 4 6 7 5 6 7 5 0 | 2 4 8 9 | --|------ 0 1 2 3 ---. x | Hence sum of the sub-matrix = 3+8+1+6+7+5 = 30 */ Query []q = {new Query(1 1 3 2) new Query(2 3 3 3) new Query(1 1 1 1)}; int m = q.Length; answerQueries(q m BIT); } } // This code is contributed by Rajput-Ji
<script> /* Javascript program to implement 2D Binary Indexed Tree 2D BIT is basically a BIT where each element is another BIT. Updating by adding v on (x y) means it's effect will be found throughout the rectangle [(x y) (max_x max_y)] and query for (x y) gives you the result of the rectangle [(0 0) (x y)] assuming the total rectangle is [(0 0) (max_x max_y)]. So when you query and update on this BITyou have to be careful about how many times you are subtracting a rectangle and adding it. Simple set union formula works here. So if you want to get the result of a specific rectangle [(x1 y1) (x2 y2)] the following steps are necessary: Query(x1y1x2y2) = getSum(x2 y2)-getSum(x2 y1-1) - getSum(x1-1 y2)+getSum(x1-1 y1-1) Here 'Query(x1y1x2y2)' means the sum of elements enclosed in the rectangle with bottom-left corner's co-ordinates (x1 y1) and top-right corner's co-ordinates - (x2 y2) Constraints -> x1<=x2 and y1<=y2 / y | | --------(x2y2) | | | | | | | | | | --------- | (x1y1) | |___________________________ (0 0) x--> In this program we have assumed a square matrix. The program can be easily extended to a rectangular one. */ let N = 4; // N-.max_x and max_y // A structure to hold the queries class Query { constructor(x1y1x2y2) { this.x1 = x1; this.y1 = y1; this.x2 = x2; this.y2 = y2; } } // A function to update the 2D BIT function updateBIT(BITxyval) { for (; x <= N; x += (x & -x)) { // This loop update all the 1D BIT inside the // array of 1D BIT = BIT[x] for (; y <= N; y += (y & -y)) BIT[x][y] += val; } return; } // A function to get sum from (0 0) to (x y) function getSum(BITxy) { let sum = 0; for(; x > 0; x -= x&-x) { // This loop sum through all the 1D BIT // inside the array of 1D BIT = BIT[x] for(; y > 0; y -= y&-y) { sum += BIT[x][y]; } } return sum; } // A function to create an auxiliary matrix // from the given input matrix function constructAux(mataux) { // Initialise Auxiliary array to 0 for (let i = 0; i <= N; i++) for (let j = 0; j <= N; j++) aux[i][j] = 0; // Construct the Auxiliary Matrix for (let j = 1; j <= N; j++) for (let i = 1; i <= N; i++) aux[i][j] = mat[N - j][i - 1]; return; } // A function to construct a 2D BIT function construct2DBIT(matBIT) { // Create an auxiliary matrix let aux = new Array(N + 1); for(let i=0;i<(N+1);i++) { aux[i]=new Array(N+1); } constructAux(mat aux); // Initialise the BIT to 0 for (let i = 1; i <= N; i++) for (let j = 1; j <= N; j++) BIT[i][j] = 0; for (let j = 1; j <= N; j++) { for (let i = 1; i <= N; i++) { // Creating a 2D-BIT using update function // everytime we/ encounter a value in the // input 2D-array let v1 = getSum(BIT i j); let v2 = getSum(BIT i j - 1); let v3 = getSum(BIT i - 1 j - 1); let v4 = getSum(BIT i - 1 j); // Assigning a value to a particular element // of 2D BIT updateBIT(BIT i j aux[i][j] - (v1 - v2 - v4 + v3)); } } return; } // A function to answer the queries function answerQueries(qmBIT) { for (let i = 0; i < m; i++) { let x1 = q[i].x1 + 1; let y1 = q[i].y1 + 1; let x2 = q[i].x2 + 1; let y2 = q[i].y2 + 1; let ans = getSum(BIT x2 y2) - getSum(BIT x2 y1 - 1) - getSum(BIT x1 - 1 y2) + getSum(BIT x1 - 1 y1 - 1); document.write('Query ('+q[i].x1+' ' +q[i].y1+' ' +q[i].x2+' ' +q[i].y2+') = ' +ans+'
'); } return; } // Driver Code let mat= [[1 2 3 4] [5 3 8 1] [4 6 7 5] [2 4 8 9]]; // Create a 2D Binary Indexed Tree let BIT = new Array(N + 1); for(let i=0;i<(N+1);i++) { BIT[i]=new Array(N+1); for(let j=0;j<(N+1);j++) { BIT[i][j]=0; } } construct2DBIT(mat BIT); /* Queries of the form - x1 y1 x2 y2 For example the query- {1 1 3 2} means the sub-matrix- y / 3 | 1 2 3 4 Sub-matrix 2 | 5 3 8 1 {1132} --. 3 8 1 1 | 4 6 7 5 6 7 5 0 | 2 4 8 9 | --|------ 0 1 2 3 ---. x | Hence sum of the sub-matrix = 3+8+1+6+7+5 = 30 */ let q = [new Query(1 1 3 2) new Query(2 3 3 3) new Query(1 1 1 1)]; let m = q.length; answerQueries(q m BIT); // This code is contributed by rag2127 </script>
תְפוּקָה
Query(1 1 3 2) = 30 Query(2 3 3 3) = 7 Query(1 1 1 1) = 6
מורכבות זמן:
שנה את שם ספריית לינוקס
- שניהם פונקציית updatebit (x y val) וגם פונקציית getsum (x y) לוקח זמן (log (n)*log (m)).
- בניית סיביות הדו -מימד לוקחת O (יומן NM (n)*יומן (M)).
- מכיוון שבכל אחת מהשאילתות אנו קוראים לפונקציה getSum (x y) כך שתענה על כל שאילתות Q O (q*log (n)*log (m)) זְמַן.
- מכאן שהמורכבות הכללית של התוכנית היא O ((nm+q)*log (n)*log (m)) אֵיפֹה
N = קואורדינטה מקסימאלית x של המטריצה כולה.
M = קואורדינטות מקסימום y של המטריצה כולה.
Q = מספר השאילתות.
שטח עזר: O (nm) לאחסן את הסיביות ואת מערך העזר
