לומדים סטטיסטיקה? אז סביר להניח ששמעת את הביטוי 'התפלגות נורמלית' בעת תיאור הנתונים. אבל מה עם הביטוי 'מוטה ימינה'? איך נראית היסטוגרמה מוטה ימינה? ומה גורם לזה?

במאמר זה, אנו נותנים לך דוגמאות של היסטוגרמות מוטות ימינה ומסבירים כיצד אלו נבדלים מגרפי התפלגות נורמליים.

תמונה תכונה: מוניקה פלייס /Wikimedia Commons

המרת אובייקט למחרוזת

מהי התפלגות נורמלית?

לפני שנסביר מה זה אומר כשנתונים מוטים נכון, בואו נסקור את ההגדרה של התפלגות נורמלית.

מיון מערכי java

עם התפלגות נורמלית, שני משתנים או יותר חולקים קשר ישיר כדי ליצור א מערך נתונים סימטרי , שעליו החצי השמאלי משקף את החצי הימני. גרפים אלה נקראים עקומות פעמון בשל צורתם המוגדרת בבירור דמוית הפעמון:

על גרף התפלגות נורמלית, הממוצע (ממוצע), החציון והמצב כולם שווים . נקודות אלו מייצגות כולן את מרכז הנתונים, או את שיא הגרף.

מה המשמעות של מוטה ימינה?

בעוד שהתפלגות נורמלית היא אחת מצורות ההתפלגות הנפוצות ביותר, לא כל מערכי הנתונים עוקבים אחר העקומה הבסיסית הזו. במילים אחרות, היסטוגרמות מסוימות מוטות ימינה או שמאלה .

התקנת לפיד

עם התפלגות מוטה ימינה (המכונה גם התפלגות 'מוטת חיובית'), רוב הנתונים נופלים לצד הימני, או החיובי, של שיא הגרף. לכן, ההיסטוגרמה מוטה באופן שהצד הימני (או ה'זנב') שלה ארוך מהצד השמאלי.

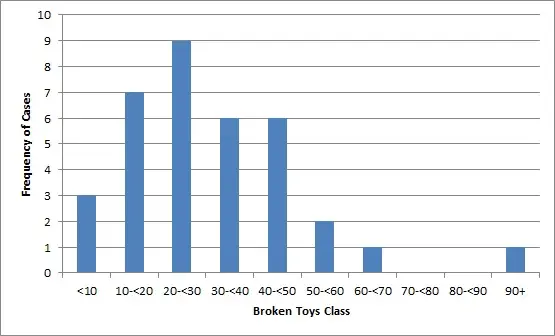
דוגמה להיסטוגרמה מוטה ימינה.

בהיסטוגרמה מוטה ימינה, הממוצע, החציון והמצב כולם שונים. במקרה זה, המצב הוא הנקודה הגבוהה ביותר של ההיסטוגרמה, בעוד שהחציון והממוצע נופלים מימין לה (או, מבחינה ויזואלית, מימין לשיא). ציין זאת הרצון המרושע תמיד להיות מימין לחציון .

גיזום אלפא בטא

גרף A מוטה ימינה ואילו גרף B מוטה שמאלה. עם גרפים מוטים ימינה, הממוצע תמיד מגיע מימין למצב (כלומר, השיא). ( אסיטגוס /Wikimedia Commons) )

תכונות אלו בסופו של דבר הופכות את זה קשה להקצות ערך טיפוסי מכיוון שאין נקודת מרכז ברורה בגרף מוטה ימינה. לעומת זאת, בהתפלגות נורמלית, מכיוון שהממוצע, החציון והמצב כולם שווים ומגיעים למרכז מערך הנתונים, אתה יכול בקלות להשתמש בערך זה כדי להכליל את הנתונים בצורה מדויקת יותר.

מה גורם להיסטוגרמה מוטה ימינה?

נתונים מוטים ימינה הם בדרך כלל תוצאה של גבול תחתון במערך נתונים (אילו נתונים מוטים שמאלה הם תוצאה של גבול גבוה יותר). אז אם הגבולות התחתונים של מערך הנתונים נמוכים במיוחד ביחס לשאר הנתונים, זה יגרום לנתונים להטות ימינה.

סיבה נוספת לעיוות היא אפקטי סטארט-אפ . לדוגמה, אם להליך יש בהתחלה הרבה הצלחות במהלך תקופת התחלה ארוכה, הדבר עלול ליצור הטיה חיובית בנתונים. (מצד הפוך, תקופת הפעלה עם מספר כשלים ראשוניים עלולה להטות את הנתונים לרעה.)