Random Forest הוא אלגוריתם למידת מכונה פופולרי השייך לטכניקת הלמידה המפוקחת. זה יכול לשמש גם לבעיות סיווג וגם לבעיות רגרסיה ב-ML. זה מבוסס על הרעיון של לימוד אנסמבל, שהוא תהליך של שילוב של מספר מסווגים לפתרון בעיה מורכבת ולשיפור ביצועי המודל.
כמו שהשם מרמז, 'Random Forest הוא מסווג המכיל מספר עצי החלטה על תת-קבוצות שונות של מערך הנתונים הנתון ולוקח את הממוצע כדי לשפר את דיוק הניבוי של מערך הנתונים הזה.' במקום להסתמך על עץ החלטות אחד, היער האקראי לוקח את החיזוי מכל עץ ומבוסס על רוב קולות התחזיות, והוא מנבא את התפוקה הסופית.
ריבוי העצים ביער מוביל לדיוק גבוה יותר ומונע את בעיית הצטיידות.
שולחן לטקס
התרשים שלהלן מסביר את פעולתו של אלגוריתם היער האקראי:
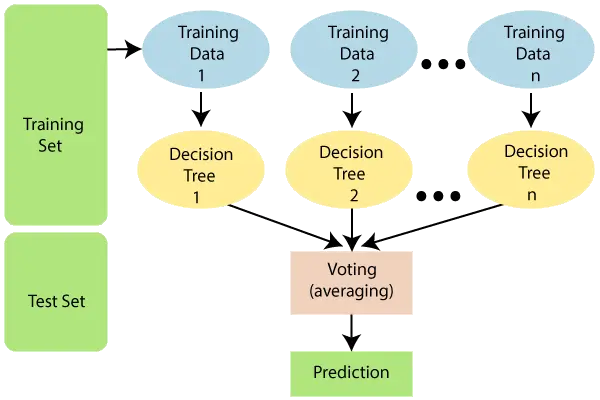
הערה: כדי להבין טוב יותר את אלגוריתם היער האקראי, עליך להיות בעל ידע באלגוריתם עץ ההחלטות.
הנחות עבור יער אקראי
מכיוון שהיער האקראי משלב עצים מרובים כדי לחזות את המחלקה של מערך הנתונים, ייתכן שעצי החלטה מסוימים עשויים לחזות את הפלט הנכון, בעוד שאחרים לא. אבל ביחד, כל העצים מנבאים את התפוקה הנכונה. לכן, להלן שתי הנחות למסווג יער אקראי טוב יותר:
- צריכים להיות כמה ערכים ממשיים במשתנה התכונה של מערך הנתונים, כך שהמסווג יוכל לחזות תוצאות מדויקות במקום תוצאה מנחשת.
- לתחזיות מכל עץ יש מתאמים נמוכים מאוד.
למה להשתמש ב-Random Forest?
להלן כמה נקודות המסבירות מדוע עלינו להשתמש באלגוריתם היער האקראי:
- זה לוקח פחות זמן אימון בהשוואה לאלגוריתמים אחרים.
- הוא חוזה פלט בדיוק גבוה, אפילו עבור מערך הנתונים הגדול שהוא רץ ביעילות.
- זה יכול גם לשמור על דיוק כאשר חלק גדול מהנתונים חסר.
כיצד פועל אלגוריתם יער אקראי?
יער אקראי פועל בשני שלבים הראשון הוא ליצור את היער האקראי על ידי שילוב של עץ החלטה של N, והשני הוא לבצע תחזיות עבור כל עץ שנוצר בשלב הראשון.
ניתן להסביר את תהליך העבודה בשלבים ובדיאגרמה שלהלן:
שלב 1: בחר אקראיות K נקודות נתונים מתוך ערכת האימונים.
שלב 2: בנה את עצי ההחלטה המשויכים לנקודות הנתונים שנבחרו (Subsets).
שלב 3: בחר את המספר N עבור עצי החלטה שברצונך לבנות.
שלב 4: חזור על שלב 1 ו-2.
שלב-5: עבור נקודות נתונים חדשות, מצא את התחזיות של כל עץ החלטות, והקצה את נקודות הנתונים החדשות לקטגוריה הזוכה בקולות הרוב.
עדכן ב-sql עם join
ניתן להבין טוב יותר את פעולת האלגוריתם על ידי הדוגמה הבאה:
דוגמא: נניח שיש מערך נתונים המכיל תמונות פירות מרובות. אז, מערך הנתונים הזה ניתן למסווג היער האקראי. מערך הנתונים מחולק לתת-קבוצות וניתן לכל עץ החלטות. במהלך שלב האימון, כל עץ החלטות מייצר תוצאת חיזוי, וכאשר מתרחשת נקודת נתונים חדשה, אז בהתבסס על רוב התוצאות, סיווג היער האקראי מנבא את ההחלטה הסופית. שקול את התמונה הבאה:

יישומים של יער אקראי
ישנם בעיקר ארבעה מגזרים שבהם נעשה שימוש בעיקר ביער אקראי:
היתרונות של יער אקראי
- Random Forest מסוגל לבצע משימות סיווג וגם משימות רגרסיה.
- הוא מסוגל להתמודד עם מערכי נתונים גדולים עם מימדיות גבוהה.
- זה משפר את הדיוק של הדגם ומונע את בעיית התאמת יתר.
חסרונות של יער אקראי
- למרות שניתן להשתמש ביער אקראי גם למשימות סיווג וגם למשימות רגרסיה, הוא לא מתאים יותר למשימות רגרסיה.
יישום פייתון של אלגוריתם יער אקראי
כעת ניישם את עץ אלגוריתם היער האקראי באמצעות Python. לשם כך, נשתמש באותו מערך נתונים 'user_data.csv', שבו השתמשנו במודלים קודמים של סיווג. על ידי שימוש באותו מערך נתונים, נוכל להשוות את מסווג היער האקראי עם מודלים סיווגים אחרים כגון מסווג עץ החלטות, KNN, SVM, רגרסיה לוגיסטית וכו'.
להלן שלבי היישום:
פיצול מחרוזות c++
- שלב עיבוד מוקדם של נתונים
- התאמת אלגוריתם היער האקראי לסט האימון
- חיזוי תוצאת הבדיקה
- בדיקת דיוק התוצאה (יצירת מטריצת בלבול)
- הדמיית תוצאת ערכת הבדיקה.
1. שלב עיבוד נתונים מראש:
להלן הקוד לשלב העיבוד המקדים:
# importing libraries import numpy as nm import matplotlib.pyplot as mtp import pandas as pd #importing datasets data_set= pd.read_csv('user_data.csv') #Extracting Independent and dependent Variable x= data_set.iloc[:, [2,3]].values y= data_set.iloc[:, 4].values # Splitting the dataset into training and test set. from sklearn.model_selection import train_test_split x_train, x_test, y_train, y_test= train_test_split(x, y, test_size= 0.25, random_state=0) #feature Scaling from sklearn.preprocessing import StandardScaler st_x= StandardScaler() x_train= st_x.fit_transform(x_train) x_test= st_x.transform(x_test)
בקוד שלמעלה, עיבדנו מראש את הנתונים. היכן טענו את מערך הנתונים, אשר ניתן כ:

2. התאמת אלגוריתם היער האקראי למערך האימונים:
כעת נתאים את אלגוריתם היער האקראי לסט האימונים. כדי להתאים אותו, נייבא את RandomForestClassifier כיתה מה sklearn.ensemble סִפְרִיָה. הקוד ניתן להלן:
#Fitting Decision Tree classifier to the training set from sklearn.ensemble import RandomForestClassifier classifier= RandomForestClassifier(n_estimators= 10, criterion='entropy') classifier.fit(x_train, y_train)
בקוד לעיל, אובייקט המסווגן מקבל את הפרמטרים הבאים:
תְפוּקָה:
RandomForestClassifier(bootstrap=True, class_weight=None, criterion='entropy', max_depth=None, max_features='auto', max_leaf_nodes=None, min_impurity_decrease=0.0, min_impurity_split=None, min_samples_leaf=1, min_samples_split=2, min_weight_fraction_leaf=0.0, n_estimators=10, n_jobs=None, oob_score=False, random_state=None, verbose=0, warm_start=False)
3. חיזוי תוצאת ערכת הבדיקות
מכיוון שהדגם שלנו מותאם לסט האימונים, אז עכשיו אנחנו יכולים לחזות את תוצאת הבדיקה. לצורך חיזוי, ניצור וקטור חיזוי חדש y_pred. להלן הקוד עבורו:
#Predicting the test set result y_pred= classifier.predict(x_test)
תְפוּקָה:
וקטור החיזוי ניתן כ:

על ידי בדיקת וקטור החיזוי לעיל והווקטור האמיתי של ערכת הבדיקה, נוכל לקבוע את התחזיות השגויות שנעשו על ידי המסווגן.
4. יצירת מטריצת הבלבול
כעת ניצור את מטריצת הבלבול כדי לקבוע את התחזיות הנכונות והלא נכונות. להלן הקוד עבורו:
q4 חודשים
#Creating the Confusion matrix from sklearn.metrics import confusion_matrix cm= confusion_matrix(y_test, y_pred)
תְפוּקָה:

כפי שאנו יכולים לראות במטריצה לעיל, יש 4+4= 8 תחזיות שגויות ו 64+28= 92 תחזיות נכונות.
5. הדמיית התוצאה של האימון
כאן נדמיין את תוצאת מערך האימונים. כדי לדמיין את תוצאת מערך האימונים, נשרטט גרף עבור מיון היער האקראי. המסווג יחזה כן או לא עבור המשתמשים שרכשו או לא רכשו את רכב השטח כפי שעשינו ברגרסיה לוגיסטית. להלן הקוד עבורו:
from matplotlib.colors import ListedColormap x_set, y_set = x_train, y_train x1, x2 = nm.meshgrid(nm.arange(start = x_set[:, 0].min() - 1, stop = x_set[:, 0].max() + 1, step =0.01), nm.arange(start = x_set[:, 1].min() - 1, stop = x_set[:, 1].max() + 1, step = 0.01)) mtp.contourf(x1, x2, classifier.predict(nm.array([x1.ravel(), x2.ravel()]).T).reshape(x1.shape), alpha = 0.75, cmap = ListedColormap(('purple','green' ))) mtp.xlim(x1.min(), x1.max()) mtp.ylim(x2.min(), x2.max()) for i, j in enumerate(nm.unique(y_set)): mtp.scatter(x_set[y_set == j, 0], x_set[y_set == j, 1], c = ListedColormap(('purple', 'green'))(i), label = j) mtp.title('Random Forest Algorithm (Training set)') mtp.xlabel('Age') mtp.ylabel('Estimated Salary') mtp.legend() mtp.show()
תְפוּקָה:

התמונה שלמעלה היא תוצאת ההדמיה עבור מיון היער האקראי שעובד עם תוצאת ערכת האימונים. זה מאוד דומה לסיווג עץ ההחלטה. כל נקודת נתונים מתאימה לכל משתמש ב-user_data, והאזורים הסגולים והירוקים הם אזורי החיזוי. האזור הסגול מסווג עבור המשתמשים שלא רכשו את רכב השטח, והאזור הירוק מיועד למשתמשים שרכשו את רכב השטח.
אז, במסווג היער האקראי, לקחנו 10 עצים שחזו כן או לא עבור המשתנה שנרכש. המסווג לקח את רוב התחזיות וסיפק את התוצאה.
6. הדמיית תוצאת ערכת הבדיקה
כעת נדמיין את תוצאת ערכת הבדיקה. להלן הקוד עבורו:
מיון מערך java
#Visulaizing the test set result from matplotlib.colors import ListedColormap x_set, y_set = x_test, y_test x1, x2 = nm.meshgrid(nm.arange(start = x_set[:, 0].min() - 1, stop = x_set[:, 0].max() + 1, step =0.01), nm.arange(start = x_set[:, 1].min() - 1, stop = x_set[:, 1].max() + 1, step = 0.01)) mtp.contourf(x1, x2, classifier.predict(nm.array([x1.ravel(), x2.ravel()]).T).reshape(x1.shape), alpha = 0.75, cmap = ListedColormap(('purple','green' ))) mtp.xlim(x1.min(), x1.max()) mtp.ylim(x2.min(), x2.max()) for i, j in enumerate(nm.unique(y_set)): mtp.scatter(x_set[y_set == j, 0], x_set[y_set == j, 1], c = ListedColormap(('purple', 'green'))(i), label = j) mtp.title('Random Forest Algorithm(Test set)') mtp.xlabel('Age') mtp.ylabel('Estimated Salary') mtp.legend() mtp.show()
תְפוּקָה:

התמונה לעיל היא תוצאת ההדמיה עבור ערכת הבדיקה. אנו יכולים לבדוק שיש מספר מינימלי של תחזיות שגויות (8) ללא בעיית Overfitting. נקבל תוצאות שונות על ידי שינוי מספר העצים במסווג.
