• Pushdown automata היא דרך ליישם CFG באותו אופן שבו אנו מעצבים DFA עבור דקדוק רגיל. DFA יכול לזכור כמות סופית של מידע, אבל מחשב כף יד יכול לזכור כמות אינסופית של מידע.
• אוטומט Pushdown הוא פשוט NFA המוגבר עם 'זיכרון מחסנית חיצוני'. התוספת של מחסנית משמשת כדי לספק יכולת ניהול זיכרון אחרון-בראשון לאוטומטי Pushdown. אוטומטיים של Pushdown יכולים לאחסן כמות בלתי מוגבלת של מידע בערימה. זה יכול לגשת לכמות מוגבלת של מידע על הערימה. מחשב כף יד יכול לדחוף אלמנט לחלק העליון של הערימה ולהוציא אלמנט מהחלק העליון של הערימה. כדי לקרוא אלמנט לתוך הערימה, יש להסיר את הרכיבים העליונים והם הולכים לאיבוד.
• מחשב כף יד חזק יותר מ-FA. כל שפה שיכולה להיות מקובלת על ידי FA יכולה להיות מקובלת גם על ידי PDA. PDA גם מקבל סוג של שפה שאפילו לא יכול להתקבל על ידי FA. לפיכך PDA הרבה יותר עדיף על FA.

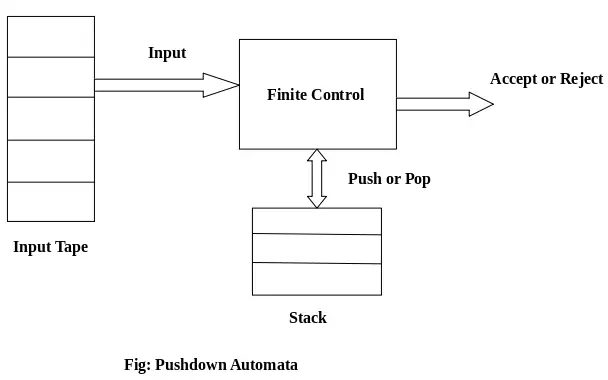
רכיבי מחשב כף יד:

קלטת קלט: קלטת הקלט מחולקת לתאים או סמלים רבים. ראש הקלט הוא לקריאה בלבד ועשוי לנוע רק משמאל לימין, סמל אחד בכל פעם.

שליטה סופית: לשלט הסופי יש איזה מצביע שמצביע על הסמל הנוכחי שיש לקרוא.

לַעֲרוֹם: הערימה היא מבנה בו אנו יכולים לדחוף ולהסיר את הפריטים מקצה אחד בלבד. יש לו גודל אינסופי. ב-PDA, הערימה משמשת לאחסון הפריטים באופן זמני.

הגדרה רשמית של מחשב כף יד:

ניתן להגדיר את ה-PDA כאוסף של 7 רכיבים:

ש: קבוצת המצבים הסופית

∑: ערכת הקלט

ג: סמל ערימה שניתן לדחוף ולהוציא מהערימה

ש0: המצב ההתחלתי

מחרוזת קלט java

עם: סמל התחלה שנמצא ב-Γ.

F: קבוצה של מצבים סופיים

ד: פונקציית מיפוי המשמשת למעבר ממצב נוכחי למצב הבא.

תיאור מיידי (מזהה)

ID הוא סימון לא רשמי של האופן שבו מחשב כף יד מחשב מחרוזת קלט ומקבל החלטה שהמחרוזת מתקבלת או נדחתה.

תיאור מיידי הוא משולש (q, w, α) כאשר:

ש מתאר את המצב הנוכחי.

ב מתאר את הקלט שנותר.

פרוס מערך java

א מתאר את תוכן הערימה, למעלה משמאל.

סימון קרוסלת:

סימן ⊢ מתאר את סימון הקרוסלה ומייצג מהלך אחד.

סימן ⊢* מתאר רצף של מהלכים.

לדוגמה,

(p, b, T) ⊢ (q, w, α)

בדוגמה שלמעלה, תוך כדי מעבר ממצב p ל-q, סמל הקלט 'b' נצרך, והחלק העליון של הערימה 'T' מיוצג על ידי מחרוזת חדשה α.

דוגמה 1:

עיצוב מחשב כף יד לקבלת שפה א^נב²ⁿ.

פִּתָרוֹן: בשפה זו, מספר n של a'ים צריך להיות ואחריו 2n מספר של b. לפיכך, ניישם היגיון פשוט מאוד, והוא אם נקרא יחיד 'a', נדחוף שני א' לערימה. ברגע שאנו קוראים 'b' אז עבור כל 'b' בודד אמור לצאת רק 'a' אחד מהערימה.

את המזהה ניתן לבנות באופן הבא:

 δ(q0, a, Z) = (q0, aaZ) δ(q0, a, a) = (q0, aaa) 

כעת כשאנו קוראים את b, נשנה את המצב מ-q0 ל-q1 ונתחיל להקפיץ 'a' מקביל. לָכֵן,

 δ(q0, b, a) = (q1, ε) 

לפיכך תהליך זה של קפיצת 'b' יחזור על עצמו אלא אם כן כל הסמלים יקראו. שים לב שפעולת הפופ מתרחשת במצב q1 בלבד.

הבמאית קארן ג'והר

 δ(q1, b, a) = (q1, ε) 

לאחר קריאת כל ה-b, כל האות התואמות אמורות להופיע. מכאן שכאשר אנו קוראים את ε כסמל קלט אז לא אמור להיות כלום בערימה. לפיכך המהלך יהיה:

 δ(q1, ε, Z) = (q2, ε) 

איפה

PDA = ({q0, q1, q2}, {a, b}, {a, Z}, δ, q0, Z, {q2})

אנו יכולים לסכם את המזהה כך:

 δ(q0, a, Z) = (q0, aaZ) δ(q0, a, a) = (q0, aaa) δ(q0, b, a) = (q1, ε) δ(q1, b, a) = (q1, ε) δ(q1, ε, Z) = (q2, ε) 

כעת נדמה את ה-PDA הזה עבור מחרוזת הקלט 'aaabbbbbb'.

פונקציית chr python

 δ(q0, aaabbbbbb, Z) ⊢ δ(q0, aabbbbbb, aaZ) ⊢ δ(q0, abbbbbb, aaaaZ) ⊢ δ(q0, bbbbbb, aaaaaaZ) ⊢ δ(q1, bbbbb, aaaaaZ) ⊢ δ(q1, bbbb, aaaaZ) ⊢ δ(q1, bbb, aaaZ) ⊢ δ(q1, bb, aaZ) ⊢ δ(q1, b, aZ) ⊢ δ(q1, ε, Z) ⊢ δ(q2, ε) ACCEPT 

דוגמה 2:

עצב מחשב כף יד לקבלת שפה 0^נ1^M0^נ.

פִּתָרוֹן: במחשב כף יד זה, n מספר של 0 עוקבים אחר כל מספר של 1 ואחריו n מספר של 0. מכאן שההיגיון לתכנון של מחשב כף יד כזה יהיה כדלקמן:

דחף את כל ה-0 אל הערימה כאשר אתה נתקל ב-0 הראשונים. אז אם אנחנו קוראים 1, פשוט אל תעשה כלום. לאחר מכן קרא 0, ובכל קריאה של 0, הקפיץ 0 אחד מהערימה.

לדוגמה:

ניתן לכתוב תרחיש זה בטופס המזהה כ:

 δ(q0, 0, Z) = δ(q0, 0Z) δ(q0, 0, 0) = δ(q0, 00) δ(q0, 1, 0) = δ(q1, 0) δ(q0, 1, 0) = δ(q1, 0) δ(q1, 0, 0) = δ(q1, ε) δ(q0, ε, Z) = δ(q2, Z) (ACCEPT state) 

כעת נדמה מחשב כף יד זה עבור מחרוזת הקלט '0011100'.

 δ(q0, 0011100, Z) ⊢ δ(q0, 011100, 0Z) ⊢ δ(q0, 11100, 00Z) ⊢ δ(q0, 1100, 00Z) ⊢ δ(q1, 100, 00Z) ⊢ δ(q1, 00, 00Z) ⊢ δ(q1, 0, 0Z) ⊢ δ(q1, ε, Z) ⊢ δ(q2, Z) ACCEPT