אשכול היררכי מתייחס להליך למידה לא מפוקח הקובע אשכולות עוקבים על סמך אשכולות שהוגדרו קודם לכן. זה עובד באמצעות קיבוץ נתונים לעץ של אשכולות. נתונים סטטיסטיים של אשכול היררכי על ידי התייחסות לכל נקודות נתונים כאשכול אינדיבידואלי. נקודת הקצה מתייחסת לקבוצה שונה של אשכולות, כאשר כל אשכול שונה מהאשכול האחר, והאובייקטים בתוך כל אשכול זהים זה לזה.

ישנם שני סוגים של מקבץ היררכי

• אשכול היררכי אגלומרטיבי
• אשכול חלוקתי

מקבץ היררכי אגלומרטיבי

מקבץ אגרסיבי הוא אחד מהסוגים הנפוצים ביותר של מקבצים היררכיים המשמשים לקיבוץ אובייקטים דומים באשכולות. מקבץ אגרסיבי ידוע גם בשם AGNES (Agglomerative Nesting). באשכולות אגרסיבית, כל נקודת נתונים פועלת כאשכול אינדיבידואלי ובכל שלב, אובייקטי נתונים מקובצים בשיטה מלמטה למעלה. בתחילה, כל אובייקט נתונים נמצא באשכול שלו. בכל איטרציה משולבים האשכולות עם אשכולות שונים עד שנוצר אשכול אחד.

אלגוריתם אשכולות היררכי אגלומרטיבי

1. קבע את הדמיון בין פרטים וכל שאר האשכולות. (מצא מטריצת קרבה).
2. שקול כל נקודת נתונים כאשכול אינדיבידואלי.
3. שלב אשכולות דומים.
4. חשב מחדש את מטריצת הקרבה עבור כל אשכול.
5. חזור על שלב 3 ושלב 4 עד שתקבל אשכול יחיד.

בואו נבין את המושג הזה בעזרת ייצוג גרפי באמצעות דנדרוגרמה.

בעזרת הדגמה נתונה, אנו יכולים להבין כיצד האלגוריתם בפועל עובד. כאן לא נעשה חישוב מתחת לכל ההנחה של הקרבה בין האשכולות.

נניח שיש לנו שש נקודות נתונים שונות P, Q, R, S, T, V.

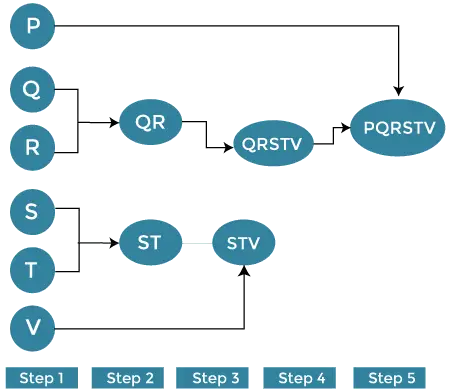
שלב 1:

ראה כל אלפבית (P, Q, R, S, T, V) כאשכול בודד ומצא את המרחק בין האשכול הבודד מכל שאר האשכולות.

שלב 2:

כעת, מיזוג את האשכולות הדומים לאשכול אחד. נניח שהאשכול Q ואשכול R דומים זה לזה כדי שנוכל למזג אותם בשלב השני. לבסוף, נקבל את האשכולות [(P), (QR), (ST), (V)]

שלב 3:

סורק ב-java

כאן, אנו מחשבים מחדש את הקרבה לפי האלגוריתם ומשלבים את שני האשכולות הקרובים ביותר [(ST), (V)] יחד כדי ליצור אשכולות חדשים כמו [(P), (QR), (STV)]

שלב 4:

חזור על אותו תהליך. האשכולות STV ו-PQ ניתנים להשוואה ומשולבים יחד ליצירת אשכול חדש. כעת יש לנו [(P), (QQRSTV)].

שלב 5:

לבסוף, שני האשכולות הנותרים מתמזגים יחד ליצירת אשכול יחיד [(PQRSTV)]

אשכול היררכי מפצל

מקבץ היררכי מחלק הוא בדיוק ההפך מאשכול היררכי אגלומרטיבי. ב-Divisive Hierarchical Clustering, כל נקודות הנתונים נחשבות לאשכול אינדיבידואלי, ובכל איטרציה, נקודות הנתונים שאינן דומות מופרדות מהאשכול. נקודות הנתונים המופרדות מטופלות כאשכול בודד. לבסוף, נשארנו עם N אשכולות.

היתרונות של אשכול היררכי

• זה פשוט ליישום ונותן את התפוקה הטובה ביותר במקרים מסוימים.
• זה קל ומביא להיררכיה, מבנה שמכיל יותר מידע.
• זה לא צריך שנציין מראש את מספר האשכולות.

חסרונות של אשכול היררכי

• זה שובר את האשכולות הגדולים.
• קשה להתמודד עם אשכולות בגדלים שונים וצורות קמורות.
• הוא רגיש לרעשים וחריגים.
• לעולם לא ניתן לשנות או למחוק את האלגוריתם ברגע שזה נעשה בעבר.