ה-Half-Adder הוא אבן בניין בסיסית של הוספת שני מספרים כשתי כניסות והפקת שתי יציאות. המוסיף משמש לביצוע פעולת OR של שני מספרים בינאריים של סיביות בודדות. ה הם מתגברים ו תוספת ביטים הם שני מצבי קלט, ו 'סחוב ' ו 'סְכוּם הם שני מצבי פלט של חצי המוסיף.
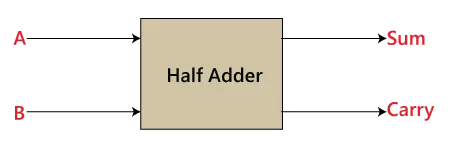
תרשים בלוקים
שולחן האמת

בטבלה למעלה,
- 'A' ו'B' הם מצבי הקלט, ו-'sum' ו'carry' הם מצבי הפלט.
- פלט ה-carrier הוא 0 במקרה בו שתי הכניסות אינן 1.
- הסיבית הפחות משמעותית של הסכום מוגדרת על ידי סיבית ה'סכום'.
טופס ה-SOP של הסכום והשאיבה הם כדלקמן:
סכום = x'y+xy'
לשאת = xy
בניית מעגל חצי אדר:
בתרשים הבלוק ראינו שהוא מכיל שתי כניסות ושתי יציאות. ה הם מתגברים ו תוספת ביטים הם מצבי הקלט, ו לשאת ו סְכוּם הם מצבי הפלט של החיבור למחצה. חצי האפעה מתוכנן בעזרת שני השערים הלוגיים הבאים:
כתב כתיבה עבור לולאה
- שער ו-2 כניסות.
- שער Exclusive-OR עם 2 כניסות או שער Ex-OR
1. שער Exclusive-OR עם 2 כניסות או שער Ex-OR
ה סְכוּם bit נוצר בעזרת ה- בלעדי-OR אוֹ לשעבר-OR שַׁעַר.

האמור לעיל הוא הסמל של EX-OR שַׁעַר. בתרשים שלמעלה, 'A' ו-'B' הם הקלט, וה-'SUMOUT' הוא התוצאה הסופית לאחר ביצוע פעולת ה-XOR של שני המספרים.
טבלת האמת של שער EX-OR היא כדלקמן:

מהטבלה לעיל, ברור ששער ה-XOR נותן את התוצאה 1 כאשר שתי הכניסות שונות. כאשר שתי הכניסות זהות, ה-XOR נותן את התוצאה 0. למידע נוסף על שער ה-XOR, לחץ כאן.
2. שער ו-2 כניסות:
שער ה-XOR אינו מסוגל להפיק את סיבית השיא. לשם כך, אנו משתמשים בשער נוסף בשם AND Gate. שער ה-AND נותן את התוצאה הנכונה של הנשיאה.

האמור לעיל הוא הסמל של ו שַׁעַר. בתרשים שלמעלה, 'A' ו-'B' הם הקלט, ו-'OUT' הוא התוצאה הסופית לאחר ביצוע פעולת AND של שני המספרים.
יש את טבלת האמת הבאה של AND Gate:

מהטבלה לעיל, ברור ששער ה-AND נותן את התוצאה 1 כאשר שתי הכניסות הן 1. כאשר שתי הכניסות שונות ו-0, שער ה-AND נותן את התוצאה 0. למידע נוסף על שער ה-AND, לחץ כאן .
מעגל לוגי של חצי מוסיף:
אז, ה-Half Adder מתוכנן על ידי שילוב של שערי 'XOR' ו-'AND' ומספק את הסכום והנשא.
מערך קוד c של מחרוזות

יש את הדבר הבא ביטוי בוליאני שֶׁל חצי מעגל Adder :
סכום= A XOR B (A+B)
Carry= A ו-B (A.B)
