תכנות דינמי היא טכניקה שמפרקת את הבעיות לתת-בעיות, ושומרת את התוצאה למטרות עתידיות כך שלא נצטרך לחשב את התוצאה שוב. תת הבעיות עוברות אופטימיזציה לאופטימיזציה של הפתרון הכולל מכונה תכונת המשנה האופטימלית. השימוש העיקרי בתכנות דינמי הוא לפתור בעיות אופטימיזציה. כאן, בעיות אופטימיזציה אומרות שכאשר אנו מנסים לגלות את הפתרון המינימלי או המקסימלי של בעיה. התכנות הדינמי מבטיח למצוא את הפתרון האופטימלי של בעיה אם הפתרון קיים.
ההגדרה של תכנות דינמי אומרת שזו טכניקה לפתרון בעיה מורכבת על ידי פריצה תחילה לאוסף של תתי-בעיות פשוטות יותר, פתרון כל תת-בעיית רק פעם אחת, ולאחר מכן אחסון הפתרונות שלהן כדי למנוע חישובים חוזרים ונשנים.
בואו נבין את הגישה הזו באמצעות דוגמה.
שקול דוגמה לסדרת פיבונאצ'י. הסדרה הבאה היא סדרת פיבונאצ'י:
פקטורי ב-ג
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, ,...
המספרים בסדרה לעיל אינם מחושבים באופן אקראי. מבחינה מתמטית, נוכל לכתוב כל אחד מהמונחים באמצעות הנוסחה שלהלן:
F(n) = F(n-1) + F(n-2),
עם ערכי הבסיס F(0) = 0, ו-F(1) = 1. כדי לחשב את המספרים האחרים, אנו עוקבים אחר הקשר לעיל. לדוגמה, F(2) הוא הסכום f(0) ו f(1), שהוא שווה ל-1.
כיצד נוכל לחשב F(20)?
האיבר F(20) יחושב באמצעות הנוסחה ה-n של סדרת פיבונאצ'י. האיור שלהלן מראה כיצד מחושב F(20).
מערך מיתרים ב-c
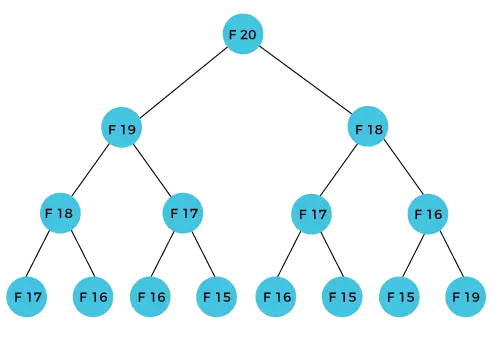
כפי שאנו יכולים לראות באיור שלעיל כי F(20) מחושב כסכום של F(19) ו-F(18). בגישת התכנות הדינמי, אנו מנסים לחלק את הבעיה לתת-בעיות דומות. אנו עוקבים אחר גישה זו במקרה הנ'ל שבו F(20) לתוך תת הבעיות הדומות, כלומר, F(19) ו-F(18). אם נסכם את ההגדרה של תכנות דינמי, זה אומר שאסור לחשב את תת הבעיה הדומה יותר מפעם אחת. ובכל זאת, במקרה הנ'ל, הבעיה מחושבת פעמיים. בדוגמה לעיל, F(18) מחושב פעמיים; באופן דומה, F(17) מחושב גם פעמיים. עם זאת, טכניקה זו שימושית למדי מכיוון שהיא פותרת את בעיות המשנה הדומות, אך אנו צריכים להיות זהירים בעת אחסון התוצאות מכיוון שאיננו מקפידים על אחסון התוצאה שחישבנו פעם אחת, אז זה יכול להוביל לבזבוז משאבים.
בדוגמה שלמעלה, אם מחשבים את ה-F(18) בתת-עץ הימני, אז זה מוביל לשימוש אדיר במשאבים ומפחית את הביצועים הכוללים.
הפתרון לבעיה שלעיל הוא לשמור את התוצאות המחושבות במערך. ראשית, אנו מחשבים את F(16) ו-F(17) ונשמור את הערכים שלהם במערך. ה-F(18) מחושב על ידי סיכום הערכים של F(17) ו-F(16), שכבר נשמרים במערך. הערך המחושב של F(18) נשמר במערך. הערך של F(19) מחושב באמצעות הסכום של F(18), ו-F(17), והערכים שלהם כבר נשמרים במערך. הערך המחושב של F(19) מאוחסן במערך. ניתן לחשב את הערך של F(20) על ידי הוספת הערכים של F(19) ו-F(18), והערכים של F(19) ו-F(18) מאוחסנים במערך. הערך המחושב הסופי של F(20) מאוחסן במערך.
איך עובדת גישת התכנות הדינמי?
להלן השלבים לפיהם התכנות הדינמי מבצע:
- זה מפרק את הבעיה המורכבת לתת-בעיות פשוטות יותר.
- הוא מוצא את הפתרון האופטימלי לבעיות המשנה הללו.
- הוא מאחסן את התוצאות של בעיות משנה (שינון). תהליך אחסון התוצאות של בעיות משנה מכונה שינון.
- הוא עושה בהם שימוש חוזר כך שאותה תת בעיה מחושבת יותר מפעם אחת.
- לבסוף, חשב את התוצאה של הבעיה המורכבת.
חמשת השלבים לעיל הם השלבים הבסיסיים לתכנות דינמי. התכנות הדינמי ישים שיש להם מאפיינים כגון:
מדהורי אמר יאללה
אותן בעיות שיש להן בעיות משנה חופפות ותתי מבנים אופטימליים. כאן, תת-מבנה אופטימלי פירושו שניתן להשיג את פתרון בעיות האופטימיזציה על ידי שילוב פשוט של הפתרון האופטימלי של כל תתי הבעיות.
במקרה של תכנות דינמי, מורכבות החלל תגדל ככל שאנו מאחסנים את תוצאות הביניים, אך מורכבות הזמן תפחת.
גישות של תכנות דינמי
קיימות שתי גישות לתכנות דינמי:
חיתוך מחרוזת javascript
- גישה מלמעלה למטה
- גישה מלמטה למעלה
גישה מלמעלה למטה
הגישה מלמעלה למטה עוקבת אחר טכניקת השינון, בעוד הגישה מלמטה למעלה עוקבת אחר שיטת הטבלציה. כאן שינון שווה לסכום הרקורסיה והמטמון. רקורסיה פירושה קריאה לפונקציה עצמה, ואילו שמירה במטמון פירושה אחסון תוצאות הביניים.
יתרונות
- זה קל מאוד להבנה ויישום.
- זה פותר את בעיות המשנה רק כאשר זה נדרש.
- קל לנפות באגים.
חסרונות
הוא משתמש בטכניקת הרקורסיה שתופסת יותר זיכרון בערימת השיחות. לפעמים כאשר הרקורסיה עמוקה מדי, מצב הצפת הערימה יתרחש.
זה תופס יותר זיכרון שפוגע בביצועים הכוללים.
בואו נבין תכנות דינמי באמצעות דוגמה.
int fib(int n) { if(n<0) error; if(n="=0)" return 0; 1; sum="fib(n-1)" + fib(n-2); } < pre> <p>In the above code, we have used the recursive approach to find out the Fibonacci series. When the value of 'n' increases, the function calls will also increase, and computations will also increase. In this case, the time complexity increases exponentially, and it becomes 2<sup>n</sup>.</p> <p>One solution to this problem is to use the dynamic programming approach. Rather than generating the recursive tree again and again, we can reuse the previously calculated value. If we use the dynamic programming approach, then the time complexity would be O(n).</p> <p>When we apply the dynamic programming approach in the implementation of the Fibonacci series, then the code would look like:</p> <pre> static int count = 0; int fib(int n) { if(memo[n]!= NULL) return memo[n]; count++; if(n<0) error; if(n="=0)" return 0; 1; sum="fib(n-1)" + fib(n-2); memo[n]="sum;" } < pre> <p>In the above code, we have used the memorization technique in which we store the results in an array to reuse the values. This is also known as a top-down approach in which we move from the top and break the problem into sub-problems.</p> <h3>Bottom-Up approach</h3> <p>The bottom-up approach is also one of the techniques which can be used to implement the dynamic programming. It uses the tabulation technique to implement the dynamic programming approach. It solves the same kind of problems but it removes the recursion. If we remove the recursion, there is no stack overflow issue and no overhead of the recursive functions. In this tabulation technique, we solve the problems and store the results in a matrix.</p> <p>There are two ways of applying dynamic programming:</p> <ul> <tr><td>Top-Down</td> </tr><tr><td>Bottom-Up</td> </tr></ul> <p>The bottom-up is the approach used to avoid the recursion, thus saving the memory space. The bottom-up is an algorithm that starts from the beginning, whereas the recursive algorithm starts from the end and works backward. In the bottom-up approach, we start from the base case to find the answer for the end. As we know, the base cases in the Fibonacci series are 0 and 1. Since the bottom approach starts from the base cases, so we will start from 0 and 1.</p> <p> <strong>Key points</strong> </p> <ul> <li>We solve all the smaller sub-problems that will be needed to solve the larger sub-problems then move to the larger problems using smaller sub-problems.</li> <li>We use for loop to iterate over the sub-problems.</li> <li>The bottom-up approach is also known as the tabulation or table filling method.</li> </ul> <p> <strong>Let's understand through an example.</strong> </p> <p>Suppose we have an array that has 0 and 1 values at a[0] and a[1] positions, respectively shown as below:</p> <img src="//techcodeview.com/img/daa-tutorial/79/dynamic-programming-2.webp" alt="Dynamic Programming"> <p>Since the bottom-up approach starts from the lower values, so the values at a[0] and a[1] are added to find the value of a[2] shown as below:</p> <img src="//techcodeview.com/img/daa-tutorial/79/dynamic-programming-3.webp" alt="Dynamic Programming"> <p>The value of a[3] will be calculated by adding a[1] and a[2], and it becomes 2 shown as below:</p> <img src="//techcodeview.com/img/daa-tutorial/79/dynamic-programming-4.webp" alt="Dynamic Programming"> <p>The value of a[4] will be calculated by adding a[2] and a[3], and it becomes 3 shown as below:</p> <img src="//techcodeview.com/img/daa-tutorial/79/dynamic-programming-5.webp" alt="Dynamic Programming"> <p>The value of a[5] will be calculated by adding the values of a[4] and a[3], and it becomes 5 shown as below:</p> <img src="//techcodeview.com/img/daa-tutorial/79/dynamic-programming-6.webp" alt="Dynamic Programming"> <p>The code for implementing the Fibonacci series using the bottom-up approach is given below:</p> <pre> int fib(int n) { int A[]; A[0] = 0, A[1] = 1; for( i=2; i<=n; i++) { a[i]="A[i-1]" + a[i-2] } return a[n]; < pre> <p>In the above code, base cases are 0 and 1 and then we have used for loop to find other values of Fibonacci series.</p> <p> <strong>Let's understand through the diagrammatic representation.</strong> </p> <p>Initially, the first two values, i.e., 0 and 1 can be represented as:</p> <img src="//techcodeview.com/img/daa-tutorial/79/dynamic-programming-7.webp" alt="Dynamic Programming"> <p>When i=2 then the values 0 and 1 are added shown as below:</p> <img src="//techcodeview.com/img/daa-tutorial/79/dynamic-programming-8.webp" alt="Dynamic Programming"> <p>When i=3 then the values 1and 1 are added shown as below:</p> <img src="//techcodeview.com/img/daa-tutorial/79/dynamic-programming-9.webp" alt="Dynamic Programming"> <p>When i=4 then the values 2 and 1 are added shown as below:</p> <img src="//techcodeview.com/img/daa-tutorial/79/dynamic-programming-10.webp" alt="Dynamic Programming"> <p>When i=5, then the values 3 and 2 are added shown as below:</p> <img src="//techcodeview.com/img/daa-tutorial/79/dynamic-programming-11.webp" alt="Dynamic Programming"> <p>In the above case, we are starting from the bottom and reaching to the top.</p> <hr></=n;></pre></0)></pre></0)>