Divide and Conquer הוא דפוס אלגוריתמי. בשיטות אלגוריתמיות, התכנון הוא לקחת מחלוקת על קלט ענק, לפרק את הקלט לחתיכות קטנות, להכריע בבעיה בכל אחת מהחתיכות הקטנות, ואז למזג את הפתרונות החתיכים לפתרון גלובלי. מנגנון זה של פתרון הבעיה נקרא אסטרטגיית Divide & Conquer.

אלגוריתם חלוקה וכבש מורכב ממחלוקת באמצעות שלושת השלבים הבאים.

לחלקהבעיה המקורית לתוך קבוצה של בעיות משנה.לִכבּוֹשׁ:פתרו כל תת-בעיית בנפרד, רקורסיבית.לְשַׁלֵב:חבר את הפתרונות של תת הבעיות כדי לקבל את הפתרון לכל הבעיה.

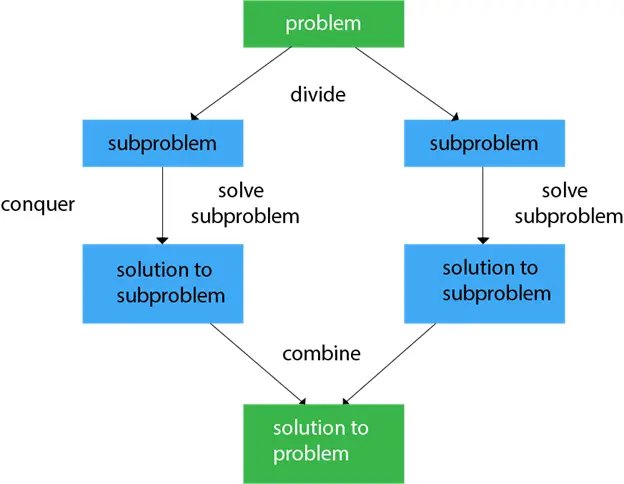
באופן כללי, אנו יכולים לעקוב אחר הפרד ומשול גישה בתהליך בן שלושה שלבים.

דוגמאות: האלגוריתמים הספציפיים של המחשב מבוססים על גישת Divide & Conquer:

1. מקסימום ומינימום בעיה
2. חיפוש בינארי
3. מיון (מיזוג מיון, מיון מהיר)
4. מגדל האנוי.

אסטרטגיית הפרד ומשול הבסיסית:

ישנם שני יסודות של אסטרטגיית הפרד וכבש:

1. נוסחת יחסים
2. מצב עצירה

1. נוסחת יחסים: זוהי הנוסחה שאנו יוצרים מהטכניקה הנתונה. לאחר יצירת הנוסחה אנו מיישמים את אסטרטגיית D&C, כלומר, אנו שוברים את הבעיה באופן רקורסיבי ופותרים את תת הבעיות השבורות.

2. מצב עצירה: כשאנחנו שוברים את הבעיה באמצעות אסטרטגיית Divide & Conquer, אז אנחנו צריכים לדעת שלכמה זמן אנחנו צריכים ליישם Divide & Conquer. אז המצב שבו הצורך לעצור את צעדי הרקורסיה שלנו של D&C נקרא מצב עצירה.

יישומים של גישת הפרד ומשול:

האלגוריתמים הבאים מבוססים על הרעיון של טכניקת ההפרדה והכיבוש:

חיפוש בינארי:אלגוריתם החיפוש הבינארי הוא אלגוריתם חיפוש, הנקרא גם חיפוש חצי מרווח או חיפוש לוגריתמי. זה עובד על ידי השוואת ערך היעד לאלמנט האמצעי הקיים במערך ממוין. לאחר ביצוע ההשוואה, אם הערך שונה, אז החצי שלא יכול להכיל את המטרה בסופו של דבר יימחק, ולאחר מכן המשך החיפוש בחצי השני. נשקול שוב את האלמנט האמצעי ונשווה אותו עם ערך היעד. התהליך ממשיך לחזור על עצמו עד לעמידה בערך היעד. אם מצאנו את החצי השני ריק לאחר סיום החיפוש, אז ניתן להסיק שהמטרה אינה קיימת במערך.מיון מהיר:זהו אלגוריתם המיון היעיל ביותר, המכונה גם מיון החלפת מחיצות. זה מתחיל בבחירת ערך ציר ממערך ואחריו חלוקת שאר רכיבי המערך לשני מערכי משנה. המחיצה נעשית על ידי השוואת כל אחד מהאלמנטים עם ערך הציר. הוא משווה אם האלמנט מחזיק ערך גדול יותר או נמוך יותר מהציר ולאחר מכן ממיין את המערכים באופן רקורסיבי.מיון מיזוג:זהו אלגוריתם מיון שממיין מערך על ידי ביצוע השוואות. זה מתחיל בחלוקת מערך לתת-מערך ולאחר מכן ממיין כל אחד מהם באופן רקורסיבי. לאחר סיום המיון, הוא ממזג אותם בחזרה.צמד הנקודות הקרוב ביותר:זו בעיה של גיאומטריה חישובית. אלגוריתם זה שם דגש על מציאת זוג הנקודות הקרוב ביותר במרחב מטרי, בהינתן n נקודות, כך שהמרחק בין צמד הנקודות צריך להיות מינימלי.האלגוריתם של שטראסן:זהו אלגוריתם לכפל מטריצה, הנקרא על שמו של וולקר שטראסן. זה הוכח כהרבה יותר מהיר מהאלגוריתם המסורתי כאשר הוא עובד על מטריצות גדולות.אלגוריתם Cooley-Tukey Fast Fourier Transform (FFT):אלגוריתם המרת פורייה מהירה נקרא על שם ג'יי ו. קולי וג'ון טורקיה. הוא עוקב אחר גישת ההפרדה והכבוש וכופה מורכבות של O(nlogn).אלגוריתם קראצובה להכפלה מהירה:זהו אחד מאלגוריתמי הכפל המהירים ביותר של הזמן המסורתי, שהומצא על ידי אנטולי קרצובה בסוף 1960 ופורסם בשנת 1962. הוא מכפיל שני מספרים n ספרות בצורה כזו על ידי הקטנתם לחד ספרתי לכל היותר.

היתרונות של הפרד וכבש

• הפרד וכבוש נוטים לפתור בהצלחה את אחת הבעיות הגדולות ביותר, כמו מגדל האנוי, פאזל מתמטי. זה מאתגר לפתור בעיות מסובכות שאין לך מושג בסיסי לגביהן, אבל בעזרת גישת ההפרד וכבוש, זה הפחית את המאמץ מכיוון שהוא עובד על חלוקת הבעיה העיקרית לשני חצאים ואז לפתור אותן באופן רקורסיבי. אלגוריתם זה מהיר בהרבה מאלגוריתמים אחרים.
• הוא משתמש ביעילות בזיכרון המטמון מבלי לתפוס מקום רב מכיוון שהוא פותר בעיות משנה פשוטות בתוך זיכרון המטמון במקום לגשת לזיכרון הראשי האיטי יותר.
• הוא מיומן יותר מזה של טכניקת ה-Brute Force המקבילה לו.
• מכיוון שהאלגוריתמים הללו מעכבים את ההקבלה, היא אינה כרוכה בשינוי כלשהו ומטופלת על ידי מערכות המשלבות עיבוד מקביל.

חסרונות של Divide and Conquer

• מכיוון שרוב האלגוריתמים שלו מתוכננים על ידי שילוב רקורסיה, כך שזה מצריך ניהול זיכרון גבוה.
• מחסנית מפורשת עלולה להשתמש יותר מדי בשטח.
• זה עלול אפילו לקרוס את המערכת אם הרקורסיה מבוצעת בצורה קפדנית יותר מהמחסנית הקיימת במעבד.