פונקציית Delete משמשת למחיקת הצומת שצוין מעץ חיפוש בינארי. עם זאת, עלינו למחוק צומת מעץ חיפוש בינארי בצורה כזו שהמאפיין של עץ החיפוש הבינארי לא יפר. ישנם שלושה מצבים של מחיקת צומת מעץ החיפוש הבינארי.
הצומת שיימחק הוא צומת עלה
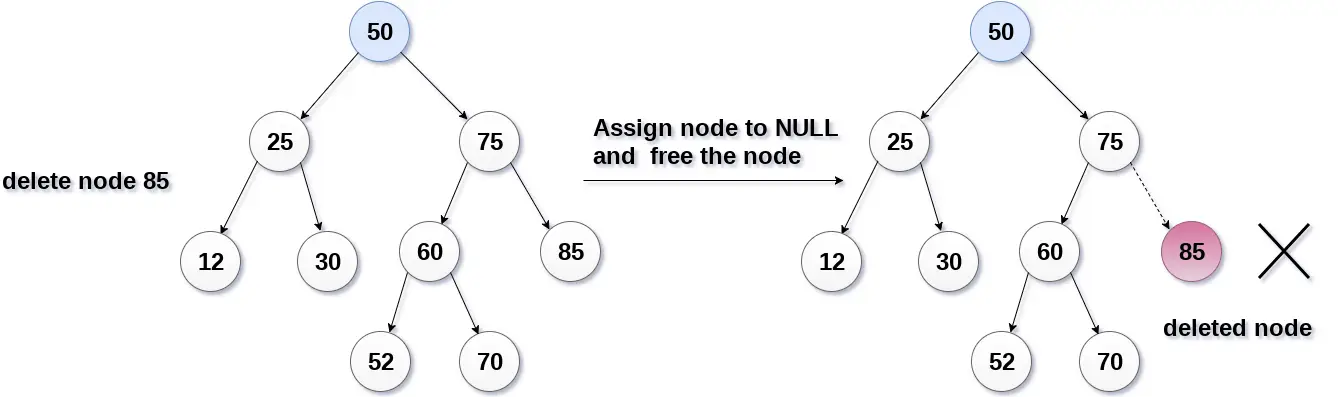
זה המקרה הפשוט ביותר, במקרה זה, החלף את צומת העלה ב-NULL ופשוט שחרר את השטח המוקצה.
עץ avl
בתמונה הבאה, אנו מוחקים את הצומת 85, מכיוון שהצומת הוא צומת עלים, לכן הצומת יוחלף ב-NULL ומרחב שהוקצה יתפנה.
לצומת שיש למחוק יש רק בן אחד.
במקרה זה, החלף את הצומת בצאצא שלו ומחק את הצומת הצאצא, שכעת מכיל את הערך שאמור להימחק. כל שעליך לעשות הוא להחליף אותו ב-NULL ולשחרר את השטח המוקצה.
בתמונה הבאה, יש למחוק את הצומת 12. יש לו רק ילד אחד. הצומת יוחלף בצומת הילד שלו והצומת המוחלף 12 (שהוא כעת צומת עלה) פשוט יימחק.

לצומת שיימחק יש שני ילדים.
זה קצת מורכב בהשוואה לשני מקרים אחרים. עם זאת, הצומת שאמור להימחק, מוחלף ביורשו או בקודמו באופן רקורסיבי עד שערך הצומת (שיימחק) מונח על עלה העץ. לאחר ההליך, החלף את הצומת ב-NULL ושחרר את השטח המוקצה.
בתמונה הבאה, יש למחוק את הצומת 50 שהוא צומת השורש של העץ. המעבר לפי הסדר של העץ המובא להלן.
6, 25, 30, 50, 52, 60, 70, 75.
שנה שם ספרייה לינוקס
החלף את 50 ביורשו לפי הסדר 52. כעת, 50 יועבר לעלה של העץ, שפשוט יימחק.

אַלגוֹרִיתְם
מחק (TREE, ITEM)
כתוב 'פריט לא נמצא בעץ' ELSE IF ITEM DATA
מחק(TREE->LEFT, ITEM)
ELSE IF ITEM > עץ -> נתונים
מחק(TREE -> RIGHT, ITEM)
אחרת אם עץ -> שמאל ועץ -> ימינה
SET TEMP = findLargestNode(TREE -> LEFT)
SET TREE -> DATA = TEMP -> DATA
מחק(TREE -> LEFT, TEMP -> DATA)
אַחֵר
SET TEMP = עץ
IF TREE -> שמאל = NULL ועץ -> ימין = NULL
SET TREE = NULL
ELSE IF TREE -> LEFT != NULL
SET TREE = עץ -> שמאל
אַחֵר
הגדר עץ = עץ -> ימינה
[סוף אם]
טמפ' חופשית
[סוף אם]
פוּנקצִיָה:
void deletion(Node*& root, int item) { Node* parent = NULL; Node* cur = root; search(cur, item, parent); if (cur == NULL) return; if (cur->left == NULL && cur->right == NULL) { if (cur != root) { if (parent->left == cur) parent->left = NULL; else parent->right = NULL; } else root = NULL; free(cur); } else if (cur->left && cur->right) { Node* succ = findMinimum(cur- >right); int val = succ->data; deletion(root, succ->data); cur->data = val; } else { Node* child = (cur->left)? Cur- >left: cur->right; if (cur != root) { if (cur == parent->left) parent->left = child; else parent->right = child; } else root = child; free(cur); } } Node* findMinimum(Node* cur) { while(cur->left != NULL) { cur = cur->left; } return cur; } 