בחלק זה, נדון בשיטה להמרת NFA ל-DFA המקביל לה. ב-NFA, כאשר ניתן קלט ספציפי למצב הנוכחי, המכונה עוברת למספר מצבים. זה יכול להיות אפס, אחד או יותר ממהלך אחד בסמל קלט נתון. מצד שני, ב-DFA, כאשר ניתן קלט ספציפי למצב הנוכחי, המכונה עוברת למצב אחד בלבד. ל-DFA יש רק מהלך אחד בסמל קלט נתון.
תן, M = (Q, ∑, δ, q0, F) הוא NFA שמקבל את השפה L(M). צריך להיות DFA שווה ערך המסומן ב-M' = (Q', ∑', q0', δ', F') כך ש-L(M) = L(M').
שלבים להמרת NFA ל-DFA:
שלב 1: בתחילה Q' = ϕ
שלב 2: הוסף q0 של NFA ל-Q'. לאחר מכן מצא את המעברים ממצב התחלה זה.
שלב 3: ב-Q', מצא את קבוצת המצבים האפשרית עבור כל סמל קלט. אם קבוצת המצבים הזו אינה ב-Q', הוסף אותה ל-Q'.
שלב 4: ב-DFA, המצב הסופי יהיה כל המדינות המכילות F (מצבים סופיים של NFA)
דוגמה 1:
המר את ה-NFA הנתון ל-DFA.
פקודת החזרה של java
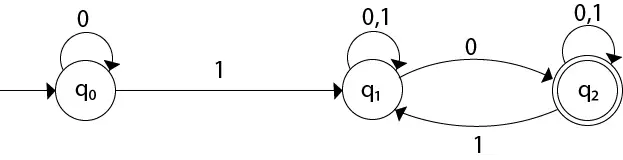
פִּתָרוֹן: עבור דיאגרמת המעבר הנתונה נבנה תחילה את טבלת המעבר.
| מדינה | 0 | 1 |
|---|---|---|
| →q0 | q0 | ש1 |
| ש1 | {q1, q2} | ש1 |
| *q2 | ש2 | {q1, q2} |
כעת נקבל מעבר δ' למצב q0.
δ'([q0], 0) = [q0] δ'([q0], 1) = [q1]
המעבר δ' עבור מצב q1 מתקבל כ:
δ'([q1], 0) = [q1, q2] (new state generated) δ'([q1], 1) = [q1]
המעבר δ' עבור מצב q2 מתקבל כ:
δ'([q2], 0) = [q2] δ'([q2], 1) = [q1, q2]
כעת נקבל מעבר δ' ב-[q1, q2].
δ'([q1, q2], 0) = δ(q1, 0) ∪ δ(q2, 0) = {q1, q2} ∪ {q2} = [q1, q2] δ'([q1, q2], 1) = δ(q1, 1) ∪ δ(q2, 1) = {q1} ∪ {q1, q2} = {q1, q2} = [q1, q2] המצב [q1, q2] הוא גם המצב הסופי מכיוון שהוא מכיל מצב סופי q2. טבלת המעבר עבור ה-DFA שנבנה תהיה:
| מדינה | 0 | 1 |
|---|---|---|
| →[q0] | [q0] | [q1] |
| [q1] | [q1, q2] | [q1] |
| *[q2] | [q2] | [q1, q2] |
| *[q1, q2] | [q1, q2] | [q1, q2] |
דיאגרמת המעבר תהיה:

ניתן לבטל את המצב q2 מכיוון ש-q2 הוא מצב בלתי ניתן להשגה.
דוגמה 2:
המר את ה-NFA הנתון ל-DFA.
שם של

פִּתָרוֹן: עבור דיאגרמת המעבר הנתונה נבנה תחילה את טבלת המעבר.
| מדינה | 0 | 1 |
|---|---|---|
| →q0 | {q0, q1} | {q1} |
| *q1 | ϕ | {q0, q1} |
כעת נקבל מעבר δ' למצב q0.
δ'([q0], 0) = {q0, q1} = [q0, q1] (new state generated) δ'([q0], 1) = {q1} = [q1] המעבר δ' עבור מצב q1 מתקבל כ:
δ'([q1], 0) = ϕ δ'([q1], 1) = [q0, q1]
כעת נקבל מעבר δ' ב-[q0, q1].
δ'([q0, q1], 0) = δ(q0, 0) ∪ δ(q1, 0) = {q0, q1} ∪ ϕ = {q0, q1} = [q0, q1] באופן דומה,
δ'([q0, q1], 1) = δ(q0, 1) ∪ δ(q1, 1) = {q1} ∪ {q0, q1} = {q0, q1} = [q0, q1] כמו ב-NFA הנתון, q1 הוא מצב סופי, ואז ב-DFA בכל מקום שבו קיים q1 המצב הזה הופך למצב סופי. מכאן שב-DFA, המצבים הסופיים הם [q1] ו-[q0, q1]. לכן קבוצה של מצבים סופיים F = {[q1], [q0, q1]}.
טבלת המעבר עבור ה-DFA שנבנה תהיה:
| מדינה | 0 | 1 |
|---|---|---|
| →[q0] | [q0, q1] | [q1] |
| *[q1] | ϕ | [q0, q1] |
| *[q0, q1] | [q0, q1] | [q0, q1] |
דיאגרמת המעבר תהיה:

אפילו אנחנו יכולים לשנות את השם של המדינות של DFA.
לְהַנִיחַ
נקודת java
A = [q0] B = [q1] C = [q0, q1]
עם השמות החדשים האלה, ה-DFA יהיה כדלקמן:

