לפני הבנה עץ ב' ו B+ עץ הבדלים, עלינו להכיר את עץ B ועץ B+ בנפרד.
מהו עץ B?
עץ ב' הוא עץ המאזן את עצמו, והוא עץ m-way שבו m מגדיר את סדר העץ. בטרי הוא הכללה של ה עץ חיפוש בינארי שבו לצומת יכולים להיות יותר ממפתח אחד ויותר משני ילדים בהתאם לערך של M . בעץ B, הנתונים מצוינים בסדר ממוין עם ערכים נמוכים יותר בתת העץ השמאלי וערכים גבוהים יותר בתת העץ הימני.
java mvc
תכונות של עץ B
להלן המאפיינים של עץ B:
- בעץ B, כל צמתי העלים חייבים להיות באותה רמה, בעוד שבמקרה של עץ בינארי, צמתי העלים יכולים להיות ברמות שונות.
בואו נבין את הנכס הזה באמצעות דוגמה.
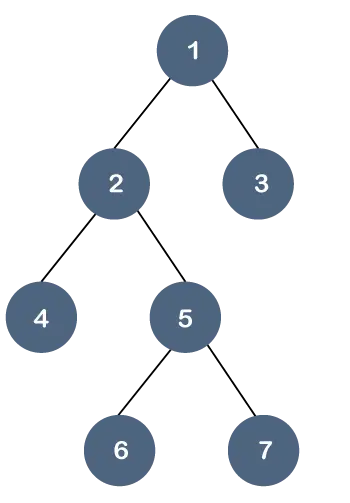
בעץ הנ'ל, כל צמתי העלים אינם באותה רמה, אך יש להם שני ילדים רבים ביותר. לכן, אנו יכולים לומר שהעץ הנ'ל הוא א עץ בינארי אבל לא עץ B.
- אם ל-Btree יש סדר של m, אז לכל צומת יכול להיות מקסימום של M במקרה של ילדים מינימליים, לצמתים העלים יש אפס ילדים, לצומת השורש שני ילדים, ולצמתים הפנימיים יש תקרה של m/2.
- לכל צומת יכולים להיות מפתחות מקסימום (m-1). לדוגמה, אם הערך של m הוא 5 אז הערך המקסימלי של מפתחות הוא 4.
- לצומת השורש יש מפתח אחד לפחות, ואילו לכל שאר הצמתים מלבד צומת השורש יש (תקרה של m/2 מינוס - 1) מפתחות מינימום.
- אם נבצע הכנסה בעץ B, אז הצומת תמיד מוכנס לצומת העלה.
נניח שאנו רוצים ליצור עץ B בסדר 3 על ידי הכנסת ערכים מ-1 עד 10.
שלב 1: ראשית, אנו יוצרים צומת עם ערך 1 כפי שמוצג להלן:

שלב 2: האלמנט הבא הוא 2, שמגיע אחרי 1 כפי שמוצג להלן:

שלב 3: האלמנט הבא הוא 3, והוא מוכנס אחרי 2 כפי שמוצג להלן:

כפי שאנו יודעים שלכל צומת יכולים להיות 2 מפתחות מקסימום, אז נחלק את הצומת הזה דרך האלמנט האמצעי. האלמנט האמצעי הוא 2, אז הוא עובר להורה שלו. לצומת 2 אין שום אב, ולכן הוא יהפוך לצומת השורש כפי שמוצג להלן:

שלב 4: האלמנט הבא הוא 4. מכיוון ש-4 גדול מ-2 ו-3, אז הוא יתווסף אחרי ה-3 כפי שמוצג להלן:

שלב 5: האלמנט הבא הוא 5. מכיוון ש-5 גדול מ-2, 3 ו-4 אז הוא יתווסף אחרי 4 כפי שמוצג להלן:

כפי שאנו יודעים שלכל צומת יכולים להיות 2 מפתחות מקסימום, אז נחלק את הצומת הזה דרך האלמנט האמצעי. האלמנט האמצעי הוא 4, אז הוא עובר להורה שלו. האב הוא צומת 2; לכן, 4 יתווספו אחרי 2 כפי שמוצג להלן:

שלב 6: האלמנט הבא הוא 6. מכיוון ש-6 גדול מ-2, 4 ו-5, אז 6 יבוא אחרי 5 כפי שמוצג להלן:

שלב 7: האלמנט הבא הוא 7. מכיוון ש-7 גדול מ-2, 4, 5 ו-6, אז 7 יבוא אחרי 6 כפי שמוצג להלן:

כפי שאנו יודעים שלכל צומת יכולים להיות 2 מפתחות מקסימום, אז נחלק את הצומת הזה דרך האלמנט האמצעי. האלמנט האמצעי הוא 6, אז הוא עובר להורה שלו כפי שמוצג להלן:

אבל, לא ניתן להוסיף 6 אחרי 4 מכיוון שלצומת יכולים להיות 2 מפתחות מקסימום, אז נחלק את הצומת הזה דרך האלמנט האמצעי. האלמנט האמצעי הוא 4, אז הוא עובר להורה שלו. מכיוון שלצומת 4 אין שום אב, צומת 4 יהפוך לצומת שורש כפי שמוצג להלן:

מהו עץ B+?
ה B+ עץ ידוע גם כעץ מאוזן עצמי מתקדם מכיוון שלכל שביל משורש העץ לעלה העץ יש אותו אורך. כאן, אותו אורך אומר שכל צמתי העלים מתרחשים באותה רמה. לא יקרה שחלק מצמת העלים מתרחשים ברמה השלישית וחלקם ברמה השנייה.
אינדקס עץ B+ נחשב לאינדקס מרובה רמות, אך מבנה העץ B+ אינו דומה לקבצים עוקבים של אינדקס רב רמות.
מדוע משתמשים בעץ B+?
עץ B+ משמש לאחסון הרשומות ביעילות רבה על ידי אחסון הרשומות בצורה אינדקסית באמצעות מבנה B+ עץ האינדקס. הודות לאינדקס הרב-שכבתי, הגישה לנתונים הופכת למהירה וקלה יותר.
B+ מבנה צומת עץ
מבנה הצומת של עץ B+ מכיל מצביעים וערכי מפתח המוצגים באיור שלהלן:

כפי שאנו יכולים לראות במבנה צומת עץ B+ לעיל שהוא מכיל n-1 ערכי מפתח (k1ל-kn-1) ו-n מצביעים (עמ'1חלק עליוןנ).
ערכי מפתח החיפוש הממוקמים בצומת נשמרים בסדר ממוין. לפיכך, אם אני
מגבלה על סוגים שונים של צמתים
תן 'b' להיות הסדר של עץ B+.
צומת ללא עלה
כתב עילית באיייר
תן 'm' מייצג את מספר הילדים של צומת, ואז היחס בין סדר העץ למספר הילדים יכול להיות מיוצג כך:

תן k לייצג את ערכי מפתח החיפוש. היחס בין סדר העץ ומפתח החיפוש יכול להיות מיוצג כך:
כפי שאנו יודעים שמספר המצביעים שווה לערכי מפתח החיפוש פלוס 1, אז מבחינה מתמטית, ניתן לכתוב אותו כך:
מספר מצביעים (או ילדים) = מספר מקשי חיפוש + 1
לכן, המספר המרבי של מצביעים יהיה 'b', ומספר המצביעים המינימלי יהיה פונקציית התקרה של b/2.
צומת עלה
צומת עלה הוא צומת המתרחש ברמה האחרונה של עץ B+, וכל צומת עלה משתמש רק במצביע אחד כדי להתחבר זה לזה כדי לספק את הגישה הרציפה ברמת העלה.
בצומת עלים, המספר המרבי של ילדים הוא:

המספר המרבי של מפתחות חיפוש הוא:

צומת שורש
המספר המרבי של ילדים במקרה של צומת השורש הוא: ב
מספר הילדים המינימלי הוא: 2
מקרים מיוחדים בעץ B+
תיק 1: אם צומת השורש הוא הצומת היחיד בעץ. במקרה זה, צומת השורש הופך לצומת העלה.
במקרה זה, המספר המרבי של ילדים הוא 1, כלומר, צומת השורש עצמו, ואילו המספר המינימלי של ילדים הוא b-1, שזהה לזה של צומת עלה.
ייצוג של צומת עלים בעץ B+

באיור שלמעלה, '.' מייצג את המצביע, בעוד שה-10, 20 ו-30 הם ערכי המפתח. המצביע מכיל את הכתובת שבה מאוחסן ערך המפתח, כפי שמוצג באיור לעיל.
דוגמה לעץ B+

באיור שלמעלה, הצומת מכיל שלושה ערכי מפתח, כלומר, 9, 16 ו-25. המצביע המופיע לפני 9, מכיל את ערכי המפתח הנמוכים מ-9 המיוצגים על ידי kאני. המצביע המופיע לפני 16, מכיל את ערכי המפתח הגדולים או שווים ל-9 אך פחות מ-16 המיוצגים על ידי kj. המצביע המופיע לפני 25, מכיל את ערכי המפתח הגדולים או שווים ל-16 אך פחות מ-25 המיוצגים על ידי kנ.
הבדלים בין עץ B לעץ B+

להלן ההבדלים בין עץ B לעץ B+:
| עץ ב' | B+ עץ |
|---|---|
| בעץ B, כל המפתחות והרשומות מאוחסנים בצמתים פנימיים וגם בצמתים עלים. | בעץ B+, מפתחות הם האינדקסים המאוחסנים בצמתים הפנימיים והרשומות מאוחסנות בצמתי העלים. |
| בעץ B, לא ניתן לאחסן מפתחות שוב ושוב, מה שאומר שאין שכפול של מפתחות או רשומות. | בעץ B+ יכולה להיות יתירות בהופעת המפתחות. במקרה זה, הרשומות מאוחסנות בצמתים העלים, ואילו המפתחות מאוחסנים בצמתים הפנימיים, כך שמפתחות מיותרים יכולים להיות נוכחים בצמתים הפנימיים. |
| ב-Btree, צמתים עלים אינם מקושרים זה לזה. | בעץ B+, צמתי העלים מקושרים זה לזה כדי לספק את הגישה הרציפה. |
| ב-Btree, החיפוש אינו יעיל במיוחד מכיוון שהרשומות מאוחסנות בצמתים עלים או פנימיים. | בעץ B+, החיפוש יעיל מאוד או מהיר יותר מכיוון שכל הרשומות מאוחסנות בצמתי העלים. |
| מחיקת צמתים פנימיים היא איטית מאוד ותהליך שלוקח זמן, מכיוון שאנו צריכים להתחשב גם בילד של המפתח שנמחק. | המחיקה בעץ B+ היא מהירה מאוד מכיוון שכל הרשומות מאוחסנות בצמתי העלים כך שאיננו צריכים להתחשב בילד של הצומת. |
| ב-Btree, גישה רציפה אינה אפשרית. | בעץ B+, כל צמתי העלים מחוברים זה לזה באמצעות מצביע, כך שגישה רציפה אפשרית. |
| ב-Btree, כמה שיותר פעולות פיצול מבוצעות שבגללן הגובה גדל בהשוואה לרוחב, | לעץ B+ יש יותר רוחב בהשוואה לגובה. |
| ב-Btree, לכל צומת יש לפחות שני ענפים וכל צומת מכיל כמה רשומות, כך שאנחנו לא צריכים לעבור עד לצמתי העלים כדי לקבל את הנתונים. | בעץ B+, צמתים פנימיים מכילים רק מצביעים וצמתי עלים מכילים רשומות. כל צמתי העלים נמצאים באותה רמה, אז אנחנו צריכים לעבור עד לצמתי העלים כדי לקבל את הנתונים. |
| צומת השורש מכיל לפחות 2 עד מ' ילדים כאשר m הוא סדר העץ. | צומת השורש מכיל לפחות 2 עד מ' ילדים כאשר m הוא סדר העץ. |
