שבר משמש לייצג את החלק של כל הדבר. לכל שאלה שני חלקים, מונה ומכנה, שכן המספר של העליון נקרא מונה ולהיפך; לדוגמה, 4/10 הוא שבר כאשר 4 הוא המונה, ו-10 הוא המכנה. בצורה ברורה יותר, ניתן דוגמאות מהחיים האמיתיים; אם מחלקים את הצ'פאטי לשני חלקים שווים, כל חלק שווה לחצי מהצ'פאטי. אז 0.04 כשבר הוא 1/25. כדי לפתור את המשוואה הזו; אנחנו צריכים לעבור שיטות שונות, אז הנה ההמרה שלב אחר שלב.
שלבים
שלב 1: מורכבת מהבעיה שתיכתב בצורת P/Q שממנה p ו-q הם מספרים שלמים חיוביים, כך שניתן לכתוב 0.04 כ-0.04/1 כדי להיות בשבר.
שלב 2 : נספור את ספרת השבר אחרי העשרוני, ובבעיה זו היא 2 לפי התהליך; נכפיל את המונה והמכנה ב-10 מתוך 0.04/1; לדוגמה, 0.55 יש 2 ספרות שבריות אז התהליך יוכפל ב-100 ואם זה יהיה 3 ספרות שבריות התהליך יוכפל ב-1000 אז עכשיו כשמגיעים לבעיה עלינו להכפיל כל אחת ב-100 של 0.04/1 .
0.04/100=004/100=4/100
שלב 3: בשלב האחרון, עלינו לפשט את השבר על ידי מציאת גורמים דומים וביטולם במידת האפשר.
4/100=1/25
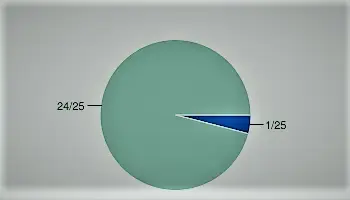
רמת דיוק עבור 0.04 כשבר
רמת הדיוק היא מספר הספרות שיש לעגל לתהליך לבחירת נקודת הדיוק הנמוכה ביותר כדי לשבור את העשרוני 0.04 עד שבריר מנקודת הדיוק עבור 0.04. 5 משמש לעגל חצי למעלה ועגול חצי למטה; אלו הן האפשרויות של הספרה למעלה ולמטה כאשר אתה משנה את נקודת הדיוק למשל 0.886 עם נקודת דיוק ל-2 מעוגלים חצי למעלה כ-89/100 וחצי למטה כ-88/100.
האם 4/100 הוא מספר מעורב, שלם או שבר תקין?
מספר מעורב מורכב ממספר שלם, ולחלק טוב מהמספר השלם המעובד אין חלקים שברים או אפילו עשרוניים; עבור השבר הנכון, המונה קטן מהמכנה. ערך המספר האמיתי של הבעיה ריק, והשבר הנכון הוא 04/100.
האם ניתן להמיר את כל הערכים העשרוניים לשברים?
התשובה היא לא מוחלט; לא ניתן להמיר את כל הספרות העשרוניות לשברים המסתיימים ערכים עשרוניים עם מספר בסיסי של ספרות אחרי הערך העשרוני, לדוגמה, 3867.9234=38679234/10000.
לערכים עשרוניים חוזרים יש מספר אחד או יותר שחוזר על עצמו אחרי הנקודה העשרונית האינסופית. לדוגמה, 9234.3333=92343333/10000=333/1000=33/100=1/3 לעגל.
אי-רציונלי עשרוני נמשך לנצח ואינו יוצר דפוס חוזר, למשל, 0.544671023...
שאלות: מרקו אכל 0.04 מעוגת יום ההולדת שלו. המיר את כמות העוגה שנצרכה לשברים בצורה הפשוטה ביותר.
תשובה: 0.04/100
004/100
1/25
סיכום
אז להמרת ערכים עשרוניים כלשהם לשברים, יש לבצע את השלבים האלה לביצוע טוב יותר של הבעיה; על ידי ביצוע שלבים אלה, אפשר גם לקבוע ערכים כלשהם, אבל כמה שיותר קשה עד בעיה במילה קשה. בכל פעם שאנו מגיעים לבעיות מסוג זה, שימו לב שכאשר שבר מופחת לצורה הפשוטה ביותר, לא ניתן לצמצם אותו עוד יותר. אם הוא מצטמצם עוד יותר, אז יש לבדוק אותו שוב לאותה תחליף, כך שזו שיטה קלה מאוד למציאת חלק השבר, מכיוון שיכולות להיות לו שאלות רבות ככל האפשר לא רק במתמטיקה אלא גם בחלקים מעשיים בפיזיקה ובכימיה. בסך הכל שיטה זו פותרת מהר יותר וקלה יותר.
תור עדיפות
