מהו שיפוע?
מספר ערכים מוחלטים המייצגים אם קו הוא תלול או שטוח יותר וה כיוון של הקו בגרף ידועים בתור a שיפוע או שיפוע. השיפוע של קו הוא מושג בסיסי בכלכלה ובמתמטיקה. זה מסומן בדרך כלל על ידי המכתב 'M'. ניתן לחשב את השיפוע על ידי חלוקת ה 'שינוי אנכי' עם ה 'שינוי אופקי' בין שתי נקודות שונות על קו.
סוגי שיפוע
ישנם שני סוגים עיקריים של מדרונות המובאים להלן:
במונחים גרפיים, שיפוע חיובי הוא שיפוע שבו הקו בגרף עולה כאשר הוא נע משמאל לימין. ניתן להבין בבירור את הרעיון של שיפוע חיובי בעזרת ה עקומת ההיצע של יצרן או חברה בכלכלה. שני המשתנים של העקומה הם מחיר בציר y וכמות סחורה בציר x. הבה נניח שהחברה מייצרת את הסחורה עבור רווח מקסימלי. לכן, כאשר מחירי הסחורה יעלו, תגדל גם הכמות שסופקה על ידי החברה של הסחורות הללו, בעוד שכאשר המחירים יורדים, הכמות שסופקה על ידי החברה תקטן. במילים אחרות, במחירים גבוהים יותר, החברה או היצרן יגדילו את הכמות המסופקת כדי להרוויח יותר רווח, בעוד שבמחירים נמוכים יותר, הם יפחיתו את הכמות שסופקה כדי להפחית את ההפסד. לפיכך, הוא מראה שהמחירים והכמות שסופקו קשורים זה לזה באופן חיובי, דבר שניתן לנקות מהתרשים המופיע להלן:
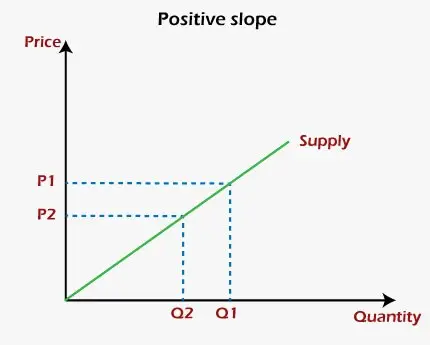
מבחינה גרפית, שיפוע שלילי הוא שיפוע שבו הקו על הגרף נופל כאשר הוא נע משמאל לימין. אחת הדוגמאות הטובות ביותר לשיפוע השלילי של הגרף היא עקומת ביקוש בכלכלה. שני המשתנים של העקומה הם מחיר בציר y וכמות סחורה בציר x. כידוע, הצרכנים קונים כמות גדולה של מוצר במחיר נמוך יותר מאשר במחיר גבוה יותר. לפיכך, הכמות הנדרשת על ידי צרכני הסחורות תפחת עם עליית מחירי הסחורות הללו. מצד שני, כאשר מחירי הסחורה ירדו, הביקוש לכמות יגדל. לפיכך, הוא מראה א מערכת יחסים שלילית בין המחירים והכמות שסופקו של סחורה זו. ניתן לנקות את זה מהתרשים המופיע להלן:

שני סוגים אחרים של שיפוע
מלבד מדרונות חיוביים ושליליים, ישנם שני סוגי מדרונות נוספים בשם שיפוע אפס ושיפוע אינסופי. ניתן להבין אותם מההסבר שניתן:
התרשים המופיע להלן הוא הצגה גרפית של שיפוע האפס:

שיפוע אינסופי מוצג בתרשים הנתון:

חישוב שיפוע
- במשוואה לינארית של ax + by + c = 0, השיפוע מוגדר כ -א/ב.
- ניתן לחשב את משוואת הקו בעזרת ה- נוסחת מדרון נקודתי אם גם השיפוע M של קו ונקודה (x1, y1) ידועים. הנוסחה ניתנת להלן:
y - y1 = m (x - x1) - שתי השורות יהיו מַקְבִּיל אם המדרונות שלהם שווה, בעוד שני קווים יהיו אֲנָכִי אם התוצר של המדרונות שלהם הוא -1.
מידע נוסף
- הערך המוחלט של השיפוע משמש כדי למצוא אם עקומה היא תלול או שטוח יותר.
- הערך החיובי והשלילי של השיפוע קובע את הכיוון, כלומר, למעלה או למטה, של המדרון.
- עקומה הופכת תלול יותר עם העלייה בערך המוחלט של השיפוע.
- עקומה הופכת מוחמא עם הירידה בערך המוחלט של השיפוע.
- תנאים אלה אינם מושפעים מה- שיפוע שלילי או חיובי (לא הערך השלילי או החיובי).
- א שיפוע חיובי נמוך יותר מרמז שתיווצר עקומה שטוחה יותר שמוטה לכיוון מעלה.
- א שיפוע חיובי גבוה יותר כלומר תיווצר עקומה תלולה יותר שכפופה לכיוון מעלה.
- א שיפוע שלילי עם ערך מוחלט גדול מרמז שתיווצר עיקול תלול יותר שמוטה לכיוון מטה.
- א שיפוע שלילי בעל ערך מוחלט קטן יותר כלומר תיווצר עקומה שטוחה יותר שכפופה לכיוון מטה.
