בהינתן מספר n מצא את כל הרצפים הבינאריים באורך 2n כך שסכום n הסיביות הראשונות זהה לסכום n הסיביות האחרונות.
דוגמאות:
עיצוב תאריך למחרוזת
Input: N = 2 Output: 0101 1111 1001 0110 0000 1010 Input: N = 3 Output: 011011 001001 011101 010001 101011 111111 110011 101101 100001 110101 001010 011110 010010 001100 000000 010100 101110 100010 110110 100100
הרעיון הוא לתקן סיביות ראשונות ואחרונות ולאחר מכן לחזור על 2*(n-1) סיביות שנותרו. ישנן ארבע אפשרויות כאשר אנו מתקנים קטעים ראשונים ואחרונים -
- הסיביות הראשונות והאחרונות הן 1 n שנותר - 1 סיביות משני הצדדים אמורות להיות גם הן באותו סכום.
- הסיביות הראשונות והאחרונות הן 0 n שנותרו - 1 סיביות משני הצדדים אמורות להיות גם הן באותו סכום.
- הסיביות הראשונה היא 1 והסיבית האחרונה היא 0 סכום של n שנותרו - 1 סיביות בצד שמאל צריכים להיות 1 פחות מהסכום n-1 סיביות בצד ימין.
- הסיביות הראשונה היא 0 והסיבית האחרונה היא סכום 1 של n שנותרו - 1 סיביות בצד שמאל צריכים להיות 1 יותר מהסכום n-1 סיביות בצד ימין.
להלן יישום הרעיון לעיל -
// C++ program to print even length binary sequences // whose sum of first and second half bits is same #include
// Java program to print even length binary // sequences whose sum of first and second // half bits is same import java.io.*; import java.util.*; class GFG { // Function to print even length binary sequences // whose sum of first and second half bits is same // diff --> difference between sums of first n bits // and last n bits // out --> output array // start --> starting index // end --> ending index static void findAllSequences(int diff char out[] int start int end) { // We can't cover difference of more // than n with 2n bits if (Math.abs(diff) > (end - start + 1) / 2) return; // if all bits are filled if (start > end) { // if sum of first n bits and // last n bits are same if (diff == 0) { System.out.print(out); System.out.print(' '); } return; } // fill first bit as 0 and last bit as 1 out[start] = '0'; out[end] = '1'; findAllSequences(diff + 1 out start + 1 end - 1); // fill first and last bits as 1 out[start] = out[end] = '1'; findAllSequences(diff out start + 1 end - 1); // fill first and last bits as 0 out[start] = out[end] = '0'; findAllSequences(diff out start + 1 end - 1); // fill first bit as 1 and last bit as 0 out[start] = '1'; out[end] = '0'; findAllSequences(diff - 1 out start + 1 end - 1); } // Driver program public static void main (String[] args) { // input number int n = 2; // allocate string containing 2*n characters char[] out = new char[2 * n + 1]; // null terminate output array out[2 * n] = '�'; findAllSequences(0 out 0 2*n - 1); } } // This code is contributed by Pramod Kumar
# Python3 program to print even length binary sequences # whose sum of first and second half bits is same # Function to print even length binary sequences # whose sum of first and second half bits is same # diff --> difference between sums of first n bits # and last n bits # out --> output array # start --> starting index # end --> ending index def findAllSequences(diff out start end): # We can't cover difference of more than n with 2n bits if (abs(diff) > (end - start + 1) // 2): return; # if all bits are filled if (start > end): # if sum of first n bits and last n bits are same if (diff == 0): print(''.join(list(out))end=' '); return; # fill first bit as 0 and last bit as 1 out[start] = '0'; out[end] = '1'; findAllSequences(diff + 1 out start + 1 end - 1); # fill first and last bits as 1 out[start] = out[end] = '1'; findAllSequences(diff out start + 1 end - 1); # fill first and last bits as 0 out[start] = out[end] = '0'; findAllSequences(diff out start + 1 end - 1); # fill first bit as 1 and last bit as 0 out[start] = '1'; out[end] = '0'; findAllSequences(diff - 1 out start + 1 end - 1); # Driver program # input number n = 2; # allocate string containing 2*n characters out=['']*(2*n); findAllSequences(0 out 0 2*n - 1); # This code is contributed by mits
// C# program to print even length binary // sequences whose sum of first and second // half bits is same using System; class GFG { // Function to print even length binary // sequences whose sum of first and // second half bits is same // diff --> difference between sums of // first n bits // and last n bits // out --> output array // start --> starting index // end --> ending index static void findAllSequences(int diff char []outt int start int end) { // We can't cover difference of // more than n with 2n bits if (Math.Abs(diff) > (end - start + 1) / 2) return; // if all bits are filled if (start > end) { // if sum of first n bits and // last n bits are same if (diff == 0) { Console.Write(outt); Console.Write(' '); } return; } // fill first bit as 0 and last bit // as 1 outt[start] = '0'; outt[end] = '1'; findAllSequences(diff + 1 outt start + 1 end - 1); // fill first and last bits as 1 outt[start] = outt[end] = '1'; findAllSequences(diff outt start + 1 end - 1); // fill first and last bits as 0 outt[start] = outt[end] = '0'; findAllSequences(diff outt start + 1 end - 1); // fill first bit as 1 and last // bit as 0 outt[start] = '1'; outt[end] = '0'; findAllSequences(diff - 1 outt start + 1 end - 1); } // Driver program public static void Main () { // input number int n = 2; // allocate string containing 2*n // characters char []outt = new char[2 * n + 1]; // null terminate output array outt[2 * n] = '�'; findAllSequences(0 outt 0 2*n - 1); } } // This code is contributed by nitin mittal.
// PHP program to print even length binary sequences // whose sum of first and second half bits is same // Function to print even length binary sequences // whose sum of first and second half bits is same // diff --> difference between sums of first n bits // and last n bits // out --> output array // start --> starting index // end --> ending index function findAllSequences($diff $out $start $end) { // We can't cover difference of more than n with 2n bits if (abs($diff) > (int)(($end - $start + 1) / 2)) return; // if all bits are filled if ($start > $end) { // if sum of first n bits and last n bits are same if ($diff == 0) print(implode(''$out).' '); return; } // fill first bit as 0 and last bit as 1 $out[$start] = '0'; $out[$end] = '1'; findAllSequences($diff + 1 $out $start + 1 $end - 1); // fill first and last bits as 1 $out[$start] = $out[$end] = '1'; findAllSequences($diff $out $start + 1 $end - 1); // fill first and last bits as 0 $out[$start] = $out[$end] = '0'; findAllSequences($diff $out $start + 1 $end - 1); // fill first bit as 1 and last bit as 0 $out[$start] = '1'; $out[$end] = '0'; findAllSequences($diff - 1 $out $start + 1 $end - 1); } // Driver program // input number $n = 2; // allocate string containing 2*n characters $out=array_fill(02*$n''); findAllSequences(0 $out 0 2*$n - 1); // This code is contributed by chandan_jnu ?> <script> // JavaScript program to print even length binary // sequences whose sum of first and second // half bits is same // Function to print even length binary // sequences whose sum of first and // second half bits is same // diff --> difference between sums of // first n bits // and last n bits // out --> output array // start --> starting index // end --> ending index function findAllSequences(diff outt start end) { // We can't cover difference of // more than n with 2n bits if (Math.abs(diff) > parseInt((end - start + 1) / 2 10)) return; // if all bits are filled if (start > end) { // if sum of first n bits and // last n bits are same if (diff == 0) { document.write(outt.join('')); document.write(' '); } return; } // fill first bit as 0 and last bit // as 1 outt[start] = '0'; outt[end] = '1'; findAllSequences(diff + 1 outt start + 1 end - 1); // fill first and last bits as 1 outt[start] = outt[end] = '1'; findAllSequences(diff outt start + 1 end - 1); // fill first and last bits as 0 outt[start] = outt[end] = '0'; findAllSequences(diff outt start + 1 end - 1); // fill first bit as 1 and last // bit as 0 outt[start] = '1'; outt[end] = '0'; findAllSequences(diff - 1 outt start + 1 end - 1); } // input number let n = 2; // allocate string containing 2*n // characters let outt = new Array(2 * n + 1); // null terminate output array outt[2 * n] = '�'; findAllSequences(0 outt 0 2*n - 1); </script>
תְפוּקָה
0101 1111 1001 0110 0000 1010
מורכבות זמן: O((4 ^ N )* N)
4^N בגלל 4 שיחות רקורסיביות ו-N (בפשטות מ-2N) עבור הזמן המושקע בהדפסת מחרוזות בגודל 2N
מרחב עזר: עַל)
ישנה גישה נוספת שבאמצעותה אנו יוצרים את כל המחרוזות האפשריות באורך n ומאחסנות אותן ברשימה באינדקס המייצג את הסכום שלהן. לאחר מכן אנו חוזרים על כל רשימה ומייצרים את המחרוזות בגודל 2n על ידי הדפסת כל מחרוזת כשכל המחרוזות האחרות ברשימה מסתכמות לאותו ערך.
C++// C++ program to implement the approach #include
// Java program to implement the approach import java.util.*; class GFG { // function that finds all the subsequences static void findAllSequences(int n) { ArrayList<ArrayList<String> > sumToString = new ArrayList<ArrayList<String> >(); for (int i = 0; i < n + 1; i++) { sumToString.add( new ArrayList<String>()); // list of strings // where index // represents sum } generateSequencesWithSum( n sumToString new ArrayList<String>() 0); permuteSequences(sumToString); } static void generateSequencesWithSum( int n ArrayList<ArrayList<String> > sumToString ArrayList<String> sequence int sumSoFar) { // Base case if there are no more binary digits to // include if (n == 0) { // add permutation to list of sequences with sum // corresponding to index String seq = ''; for (int i = 0; i < sequence.size(); i++) { seq = seq + sequence.get(i); } ArrayList<String> x = sumToString.get(sumSoFar); x.add(seq); sumToString.set(sumSoFar x); return; } // Generate sequence +0 sequence.add('0'); generateSequencesWithSum(n - 1 sumToString sequence sumSoFar); sequence.remove(0); // Generate sequence +1 sequence.add('1'); generateSequencesWithSum(n - 1 sumToString sequence sumSoFar + 1); sequence.remove(0); } // function to form permutations of the sequences static void permuteSequences( ArrayList<ArrayList<String> > sumToString) { // There are 2^n substring in this list of lists for (int sumIndexArr = 0; sumIndexArr < sumToString.size(); sumIndexArr++) { // Append for (int sequence1 = 0; sequence1 < sumToString.get(sumIndexArr).size(); sequence1++) { for (int sequence2 = 0; sequence2 < sumToString.get(sumIndexArr).size(); sequence2++) { if (sumIndexArr == sumToString.size() - 1 && sequence1 == sumToString .get(sumIndexArr) .size() - 1 && sequence2 == sumToString .get(sumIndexArr) .size() - 1) { System.out.print('1111'); } else { System.out.println( sumToString.get(sumIndexArr) .get(sequence1) + sumToString.get(sumIndexArr) .get(sequence2)); } } } } } // Driver Code public static void main(String[] args) { // Function Call findAllSequences(2); } // this code is contributed by phasing17 }
def findAllSequences(n): sumToString = [[] for x in range(n+1)] # list of strings where index represents sum generateSequencesWithSum(n sumToString [] 0) permuteSequences(sumToString) def generateSequencesWithSum(n sumToString sequence sumSoFar): #Base case if there are no more binary digits to include if n == 0: sumToString[sumSoFar].append(''.join(sequence)) #add permutation to list of sequences with sum corresponding to index return #Generate sequence +0 sequence.append('0') generateSequencesWithSum(n-1 sumToString sequence sumSoFar) sequence.pop() #Generate sequence +1 sequence.append('1') generateSequencesWithSum(n-1 sumToString sequence sumSoFar+1) sequence.pop() def permuteSequences(sumToString): #There are 2^n substring in this list of lists for sumIndexArr in sumToString: # Append for sequence1 in sumIndexArr: for sequence2 in sumIndexArr: print(sequence1 + sequence2) findAllSequences(2) #Contribution by Xavier Jean Baptiste
using System; using System.Collections.Generic; class GFG { static void findAllSequences(int n) { List<List<string>> sumToString = new List<List<string>>(); for(int i = 0; i < n + 1; i++) { sumToString.Add(new List<string>()); // list of strings where index represents sum } generateSequencesWithSum(n sumToString new List<string>() 0); permuteSequences(sumToString); } static void generateSequencesWithSum(int n List<List<string>> sumToString List<string> sequence int sumSoFar) { // Base case if there are no more binary digits to include if(n == 0) { //add permutation to list of sequences with sum corresponding to index string seq = ''; for(int i = 0; i < sequence.Count; i++) { seq = seq + sequence[i]; } sumToString[sumSoFar].Add(seq); return; } // Generate sequence +0 sequence.Add('0'); generateSequencesWithSum(n-1 sumToString sequence sumSoFar); sequence.RemoveAt(0); // Generate sequence +1 sequence.Add('1'); generateSequencesWithSum(n-1 sumToString sequence sumSoFar+1); sequence.RemoveAt(0); } static void permuteSequences(List<List<string>> sumToString) { // There are 2^n substring in this list of lists for(int sumIndexArr = 0; sumIndexArr < sumToString.Count; sumIndexArr++) { // Append for(int sequence1 = 0; sequence1 < sumToString[sumIndexArr].Count; sequence1++) { for(int sequence2 = 0; sequence2 < sumToString[sumIndexArr].Count; sequence2++) { if(sumIndexArr == sumToString.Count-1 && sequence1 == sumToString[sumIndexArr].Count-1 && sequence2 == sumToString[sumIndexArr].Count-1) { Console.Write('1111'); } else { Console.WriteLine(sumToString[sumIndexArr][sequence1] + sumToString[sumIndexArr][sequence2]); } } } } } static void Main() { findAllSequences(2); } } // This code is contributed by divyesh072019.
<script> function findAllSequences(n) { let sumToString = []; for(let i = 0; i < n + 1; i++) { sumToString.push([]); // list of strings where index represents sum } generateSequencesWithSum(n sumToString [] 0); permuteSequences(sumToString); } function generateSequencesWithSum(n sumToString sequence sumSoFar) { // Base case if there are no more binary digits to include if(n == 0) { //add permutation to list of sequences with sum corresponding to index sumToString[sumSoFar].push(sequence.join('')); return; } // Generate sequence +0 sequence.push('0'); generateSequencesWithSum(n-1 sumToString sequence sumSoFar); sequence.shift(); // Generate sequence +1 sequence.push('1'); generateSequencesWithSum(n-1 sumToString sequence sumSoFar+1); sequence.shift(); } function permuteSequences(sumToString) { // There are 2^n substring in this list of lists for(let sumIndexArr = 0; sumIndexArr < sumToString.length; sumIndexArr++) { // Append for(let sequence1 = 0; sequence1 < sumToString[sumIndexArr].length; sequence1++) { for(let sequence2 = 0; sequence2 < sumToString[sumIndexArr].length; sequence2++) { if(sumIndexArr == sumToString.length-1 && sequence1 == sumToString[sumIndexArr].length-1 && sequence2 == sumToString[sumIndexArr].length-1) { document.write('1111'); } else { document.write(sumToString[sumIndexArr][sequence1] + sumToString[sumIndexArr][sequence2] + ''); } } } } } findAllSequences(2); // This code is contributed by decode2207. </script>
תְפוּקָה
0000 0101 0110 1001 1010 1111
ניתוח מורכבות הזמן:
generSequencesWithSum = O((2נ)*N)
- 2נ: אנו יוצרים את כל התמורות של מחרוזות בינאריות בגודל N
- N: המר את רשימת התווים למחרוזת ושמור במערך. זה נעשה במקרה הבסיסי.
permuteSequences = O((2נ) * N!/(N/2)!2*נ)
- 2נ: אנו חוזרים על כל המחרוזת שנוצרה בגודל n
- N!/(N/2)!2: זה קצת מאתגר להסביר
ניקח N = 2 כדוגמה. המערך שלנו של רצף אפשרי של גודל n יהיה:
| אינדקס מערך | 1 | 2 | |
| רשימה של מחרוזות | 00 | 0110 | 11 |
ברשימת המחרוזות שהאינדקס מייצג את הסכום נקבל את ספירת המחרוזות בגודל 2n על ידי שימוש בנוסחת 'n בחר k'. במקרה שלנו זה יהיה nCk *nCk שבו k מייצג את מספר ה-1 בכל חצי של המחרוזת בגודל 2n:
k = 0 יש לנו (2C0)^2 = מחרוזת אחת (0000)
k = 1 יש לנו (2C1)^2 מחרוזת = 4 מחרוזות(0101 0110 1001 1010)
k = 2 יש לנו (2c2)^2 = מחרוזת אחת (1111)
מצביע הפנייה
אנו מקבלים את רשימת המחרוזת הארוכה ביותר שלנו כאשר k = N/2 מכאןנגN/2= N!/[(N/2)! * (N - N/2)!] מה שמפשט לנגN/2= N!/(N/2)!2
מכאן שלכל אלמנט עלינו לעבור דרכו לכל היותרנגN/2ליצירת מיתרים באורך 2N
ללא הוכחה רשמית אם נרשום גרף 2^N ו-N!/(N/2)!2אנחנו רואים את זה 2נבעל קצב צמיחה מהיר יותר מזה האחרון. לכן O(2נ* N!/(N/2)2)< O(2נ*2נ) = O(22n) = O(4נ)
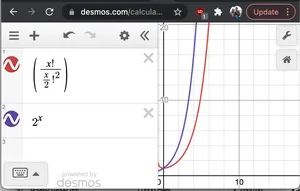 גרף של 2^x ו-nC(n/2)
גרף של 2^x ו-nC(n/2)- N: עלינו להדפיס כל מחרוזת בגודל 2N
לבסוף נוכל להתעלם ממורכבות הזמן של generSequencesWithSum מכיוון ש-permuteSequence הוא המונח המוביל
מורכבות הזמן: O(2נ* N!/(N/2)!2* N) (טוב יותר מהפתרון הראשון של O((4^N) * N ראה הסבר למעלה לפרטים נוספים)
חלל עזר : O(2נ) מכיוון שאנו מאחסנים את כל תמורות המחרוזות הבינאריות בגודל N
יוניקס לעומת חלונות
#include
import java.util.*; class GFG { static class FirstHalf { String data; int sum; FirstHalf(String data int sum) { this.data = data; this.sum = sum; } } //MAP: Key -> sum of bits; Value -> All possible permutation with respective sum static Map<Integer ArrayList<String>> map = new HashMap<>(); //first N-half bits static List<FirstHalf> firstHalf = new ArrayList<>(); //function to find sum of the bits from a String public static int sumOfString(String s) { int sum = 0; //ex: converts '1' to 1 -> (ASCII('1') - ASCII('0') = 1) for(char c: s.toCharArray()) { sum += c - '0'; } return sum; } public static void perm(String p char[] bin int level int n) { //p: processed string(processed permutation at current level) //bin: {'0' '1'} //l: current level of recursion tree (leaf/solution level = 0) //n: total levels if(level == 0) { //at solution level find sum of the current permutation int sum = sumOfString(p); //store current permutation to firstHalf list firstHalf.add(new FirstHalf(p sum)); //put current permutation to its respective sum value map.putIfAbsent(sum new ArrayList<String>()); map.get(sum).add(p); return; } //generate calls for permutation //working: first solution with all 0s then replacing last 0 with 1 and so on... for(char c: bin) { perm(p+c bin level-1 n); } } public static void result() { int i = 0; for(FirstHalf first: firstHalf) { //for each firstHalf string //find sum of the bits of current string int sum = first.sum; //retrieve respective secondHalf from map based on sum key ArrayList<String> secondHalf = map.get(sum); for(String second: secondHalf) { //append first and second half and print System.out.print(first.data+second+' '); //after every 6 solution line is changed in output //only for formatting below lines could be removed i++; if(i % 6 == 0) System.out.println(); } } } public static void main(String[] args) { char[] up = {'0' '1'}; int n = 2; perm('' up n n); result(); } } //Code contributed by Animesh Singh
# Python code implementation class FirstHalf: def __init__(self data sum): self.data = data self.sum = sum # MAP: Key -> sum of bits; Value -> All possible permutation with respective sum map = {} # first N-half bits firstHalf = [] # function to find sum of the bits from a String def sumOfString(s): sum = 0 # ex: converts '1' to 1 -> (ASCII('1') - ASCII('0') = 1) for i in range(len(s)): sum += ord(s[i]) - ord('0') return sum def perm(p bin level n): # p: processed string(processed permutation at current level) # bin: ['0' '1'] # l: current level of recursion tree (leaf/solution level = 0) # n: total levels if level == 0: # at solution level find sum of the current permutation sum = sumOfString(p) # store current permutation to firstHalf list firstHalf.append(FirstHalf(p sum)) # put current permutation to its respective sum value if sum not in map: map[sum] = [] map[sum].append(p) return # generate calls for permutation # working: first solution with all 0s then replacing last 0 with 1 and so on... for i in range(len(bin)): perm(p+bin[i] bin level-1 n) def result(): i = 0 for j in range(len(firstHalf)): # for each firstHalf string # find sum of the bits of current string sum = firstHalf[j].sum # retrieve respective secondHalf from map based on sum key secondHalf = map[sum] for k in range(len(secondHalf)): # append first and second half and print print(firstHalf[j].data + secondHalf[k] + ' ' end='') # after every 6 solution line is changed in output # only for formatting below lines could be removed i = i + 1 if(i % 6 == 0): print('n') up = ['0' '1'] n = 2 perm('' up n n) result() # The code is contributed by Nidhi goel.
using System; using System.Collections.Generic; class FirstHalf { public string data; public int sum; public FirstHalf(string data int sum) { this.data = data; this.sum = sum; } } class Gfg { // MAP: Key -> sum of bits; Value -> All possible permutation with respective sum static Dictionary<int List<string>> mp = new Dictionary<int List<string>>(); // first N-half bits static List<FirstHalf> firstHalf = new List<FirstHalf>(); // function to find sum of the bits from a String static int sumOfString(string s) { int sum = 0; // ex: converts '1' to 1 -> (ASCII('1') - ASCII('0') = 1) foreach (char c in s) { sum += (c - '0'); } return sum; } static void perm(string p char[] bin int level int n) { // p: processed string(processed permutation at current level) // bin: {'0' '1'} // l: current level of recursion tree (leaf/solution level = 0) // n: total levels if (level == 0) { // at solution level find sum of the current permutation int sum = sumOfString(p); // store current permutation to firstHalf list firstHalf.Add(new FirstHalf(p sum)); // put current permutation to its respective sum value if (mp.ContainsKey(sum)) { mp[sum].Add(p); } else { mp.Add(sum new List<string> { p }); } return; } // generate calls for permutation // working: first solution with all 0s // then replacing last 0 with 1 and so on... for (int i = 0; i < n; i++) { char c = bin[i]; perm(p + c bin level - 1 n); } } static void result() { int i = 0; foreach (FirstHalf first in firstHalf) { // for each firstHalf string // find sum of the bits of current string int sum = first.sum; // retrieve respective secondHalf from map based on sum key List<string> secondHalf = mp[sum]; foreach (string second in secondHalf) { // append first and second half and print Console.Write(first.data + second + ' '); // after every 6 solution line is changed in output // only for formatting below lines could be removed i++; if (i % 6 == 0) Console.WriteLine(); } } } static void Main(string[] args) { char[] up = { '0' '1' }; int n = 2; string x = ''; perm(x up n n); result(); } }
class FirstHalf { constructor(data sum) { this.data = data; this.sum = sum; } } // MAP: Key -> sum of bits; Value -> All possible permutation with respective sum const map = new Map(); // first N-half bits const firstHalf = []; // function to find sum of the bits from a String function sumOfString(s) { let sum = 0; //ex: converts '1' to 1 -> (ASCII('1') - ASCII('0') = 1) for(let i = 0; i < s.length; i++) { sum += s.charCodeAt(i) - '0'.charCodeAt(0); } return sum; } function perm(p bin level n) { // p: processed string(processed permutation at current level) // bin: ['0' '1'] // l: current level of recursion tree (leaf/solution level = 0) // n: total levels if(level == 0) { // at solution level find sum of the current permutation let sum = sumOfString(p); // store current permutation to firstHalf list firstHalf.push(new FirstHalf(p sum)); // put current permutation to its respective sum value if(!map.has(sum)) map.set(sum []); map.get(sum).push(p); return; } // generate calls for permutation // working: first solution with all 0s then replacing last 0 with 1 and so on... for(let i = 0; i < bin.length; i++) { perm(p+bin[i] bin level-1 n); } } function result() { let i = 0; for(let j = 0; j < firstHalf.length; j++) { // for each firstHalf string // find sum of the bits of current string let sum = firstHalf[j].sum; // retrieve respective secondHalf from map based on sum key let secondHalf = map.get(sum); for(let k = 0; k < secondHalf.length; k++) { // append first and second half and print process.stdout.write(firstHalf[j].data + secondHalf[k] + ' '); // after every 6 solution line is changed in output // only for formatting below lines could be removed i++; if(i % 6 == 0) process.stdout.write('n'); } } } const up = ['0' '1']; const n = 2; perm('' up n n); result();
תְפוּקָה
0000 0101 0110 1001 1010 1111
אַלגוֹרִיתְם:
1. צור את כל התמורות הבינאריות בגודל n
2. חשב את סכום הביטים של כל תמורה וזכור אותו למחצית השנייה
[לדוגמה: עבור n=2 זכור שיש שתי מחרוזות עם סכום = 1 כלומר '01' '10' ]
3. חזרו על כל התמורות שנוצרו ולכל אחת מהן צרף את המחצית השנייה לפי סכום הביטים
ניתוח מורכבות הזמן:
מחרוזות משרשרות java
sumOfString() = O(N) : חצו כל סיביות והוסיפו אותה לסכום
Perm() = O(2נ*נ)
2N * N : אנו יוצרים את כל התמורות של סיביות בינאריות בגודל N ומוצאים את סכום הסיביות עבור כל תמורה
תוֹצָאָה() = O((2נ) * (N!/(N/2)!)2)
2נ: אנו חוזרים על כל התמורות האפשריות בגודל N (חצי ראשון)
NCN/2 = N!/(N/2)!2: (גודל מקסימלי שני-חצי) : הסבר למטה:
ניקח N = 4 כדוגמה.:
//Hash-Map נראה כמו
0 -> [0000] ................................ (גודל רשימה: 4C0 = 1)
1 -> [0001 0010 0100 1000] ................................ (גודל רשימה: 4C1 = 4)
2 -> [0011 0101 0110 1001 1010 1100] ................................ (גודל רשימה: 4C2 = 6)
3 -> [0111 1011 1101 1110] ................................ (גודל רשימה: 4C3 = 4)
4 -> [1111] ................................( גודל רשימה: 4C4 = 1)
אנו רואים כאן שלכל רשימה יש גודל של N בחר מפתח אשר יהיה מקסימום ב-N בחר N/2
מכיוון שאנו חוזרים על כל ה-2נתמורות והוספה של מחצית שנייה מהמפה. למפה יש את הרשימה בגודל המקסימלי במיקום N/2.
המקרה הגרוע ביותר מתרחש במצב N/2 שבו עלינו לעבור NCN/2 = N!/(N/2)!2תמורות.
מנהל משימות עבור לינוקס
מורכבות הזמן: O(2נ* N!/(N/2)!2)
רווח עזר: O(2נ) מכיוון שאנו מאחסנים את כל תמורות המחרוזות הבינאריות בגודל N
