דוגמה 1:
עצב NFA עבור טבלת המעבר כמפורט להלן:
| מצב נוכחי | 0 | 1 |
|---|---|---|
| →q0 | q0, q1 | q0, q2 |
| ש1 | ש3 | ה |
| ש2 | q2, q3 | ש3 |
| →q3 | ש3 | ש3 |
פִּתָרוֹן:
ניתן לשרטט את דיאגרמת המעבר באמצעות פונקציית המיפוי כפי שמוצגת בטבלה.
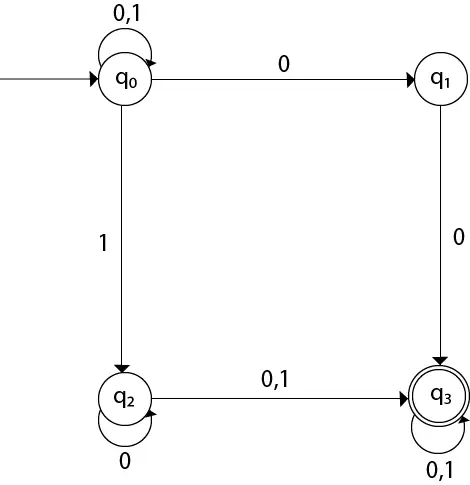
כאן,
b+ עץ
δ(q0, 0) = {q0, q1} δ(q0, 1) = {q0, q2} Then, δ(q1, 0) = {q3} Then, δ(q2, 0) = {q2, q3} δ(q2, 1) = {q3} Then, δ(q3, 0) = {q3} δ(q3, 1) = {q3} דוגמה 2:
עצב NFA עם ∑ = {0, 1} מקבל את כל המחרוזות המסתיימות ב-01.
פִּתָרוֹן:

לפיכך, NFA יהיה:
מדהובלה

דוגמה 3:
עצב NFA עם ∑ = {0, 1} שבו כפול '1' ואחריו כפול '0'.
פִּתָרוֹן:
ה-FA עם כפול 1 הוא כדלקמן:

יש לבוא מיד אחריו כפול 0.
לאחר מכן,

עכשיו לפני כפול 1, יכולה להיות כל מחרוזת של 0 ו-1. באופן דומה, אחרי כפול 0, יכולה להיות כל מחרוזת של 0 ו-1.
מכאן שה-NFA הופך:

עכשיו שוקלים את המחרוזת 01100011
q0 → q1 → q2 → q3 → q4 → q4 → q4 → q4
דוגמה 4:
עצב NFA שבו כל המחרוזת מכילה מחרוזת משנה 1110.
מיון רשימת מערך java
פִּתָרוֹן:
השפה מורכבת מכל המחרוזת המכילה תת-מחרוזת 1010. דיאגרמת המעבר החלקית יכולה להיות:

עכשיו כמו 1010 יכול להיות המחרוזת המשנה. לפיכך נוסיף את הכניסות 0 ו-1 כדי שניתן יהיה לשמור על המחרוזת המשנה 1010 של השפה. מכאן שה-NFA הופך:
רשימת ג'אווה

ניתן לתת טבלת מעבר לתרשים המעבר לעיל להלן:
| מצב נוכחי | 0 | 1 |
|---|---|---|
| →q1 | ש1 | ש1, ש2 |
| ש2 | ש3 | |
| ש 3 | ש 4 | |
| ש 4 | ש5 | *q5 | ש5 | ש5 |
שקול מחרוזת 111010,
δ(q1, 111010) = δ(q1, 1100) = δ(q1, 100) = δ(q2, 00)
נתקע! מכיוון שאין נתיב מ-q2 עבור סמל קלט 0. אנו יכולים לעבד מחרוזת 111010 בדרך אחרת.
δ(q1, 111010) = δ(q2, 1100) = δ(q3, 100) = δ(q4, 00) = δ(q5, 0) = δ(q5, ε)
כמצב q5 הוא מצב הקבלה. אנחנו מקבלים את הסריקה המלאה, והגענו למצב הסופי.
דוגמה 5:
עצב NFA עם ∑ = {0, 1} מקבל את כל המחרוזת שבה הסמל השלישי מהקצה הימני הוא תמיד 0.
פִּתָרוֹן:

כך אנו מקבלים את הסמל השלישי מהקצה הימני כ-'0' תמיד. ה-NFA יכול להיות:

התמונה שלמעלה היא NFA מכיוון שבמצב q0 עם קלט 0, נוכל לעבור למצב q0 או q1.
