אלגוריתם בלמן פורד הוא אלגוריתם הנתיב הקצר ביותר במקור יחיד. אלגוריתם זה משמש למציאת המרחק הקצר ביותר מהקודקוד הבודד לכל שאר הקודקודים של גרף משוקלל. ישנם אלגוריתמים שונים אחרים המשמשים למציאת הנתיב הקצר ביותר כמו אלגוריתם דיקסטרה וכו'. אם הגרף המשוקלל מכיל את ערכי המשקל השליליים, אז האלגוריתם של דיקסטרה אינו מאשר אם הוא מייצר את התשובה הנכונה או לא. בניגוד לאלגוריתם דיקסטרה, אלגוריתם bellman ford מבטיח את התשובה הנכונה גם אם הגרף המשוקלל מכיל את ערכי המשקל השליליים.
כלל האלגוריתם הזה
We will go on relaxing all the edges (n - 1) times where, n = number of vertices
שקול את הגרף שלהלן:
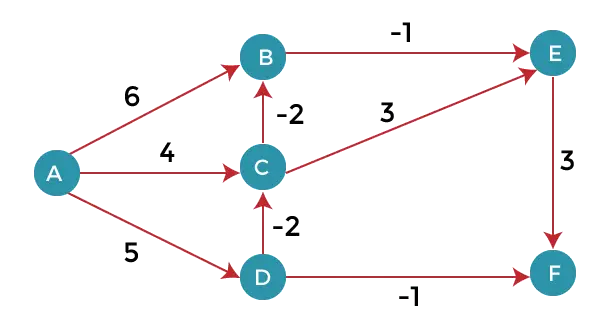
כפי שאנו יכולים לראות בגרף לעיל שחלק מהמשקלים הם שליליים. הגרף שלמעלה מכיל 6 קודקודים אז נמשיך להירגע עד 5 הקודקודים. כאן, נרגע את כל הקצוות 5 פעמים. הלולאה תחזור על עצמה 5 פעמים כדי לקבל את התשובה הנכונה. אם הלולאה חוזרת יותר מ-5 פעמים אז גם התשובה תהיה זהה, כלומר, לא יהיה שינוי במרחק בין הקודקודים.
מרגיע פירושו:
החלפת זיכרון
If (d(u) + c(u , v) <d(v)) d(v)="d(u)" + c(u , v) < pre> <p>To find the shortest path of the above graph, the first step is note down all the edges which are given below:</p> <p>(A, B), (A, C), (A, D), (B, E), (C, E), (D, C), (D, F), (E, F), (C, B)</p> <p>Let's consider the source vertex as 'A'; therefore, the distance value at vertex A is 0 and the distance value at all the other vertices as infinity shown as below:</p> <img src="//techcodeview.com/img/daa-tutorial/85/bellman-ford-algorithm-2.webp" alt="Bellman-Ford Algorithm"> <p>Since the graph has six vertices so it will have five iterations.</p> <p> <strong>First iteration</strong> </p> <p>Consider the edge (A, B). Denote vertex 'A' as 'u' and vertex 'B' as 'v'. Now use the relaxing formula:</p> <p>d(u) = 0</p> <p>d(v) = ∞</p> <p>c(u , v) = 6</p> <p>Since (0 + 6) is less than ∞, so update</p> <pre> d(v) = d(u) + c(u , v) </pre> <p>d(v) = 0 + 6 = 6</p> <p>Therefore, the distance of vertex B is 6.</p> <p>Consider the edge (A, C). Denote vertex 'A' as 'u' and vertex 'C' as 'v'. Now use the relaxing formula:</p> <p>d(u) = 0</p> <p>d(v) = ∞</p> <p>c(u , v) = 4</p> <p>Since (0 + 4) is less than ∞, so update</p> <pre> d(v) = d(u) + c(u , v) </pre> <p>d(v) = 0 + 4 = 4</p> <p>Therefore, the distance of vertex C is 4.</p> <p>Consider the edge (A, D). Denote vertex 'A' as 'u' and vertex 'D' as 'v'. Now use the relaxing formula:</p> <p>d(u) = 0</p> <p>d(v) = ∞</p> <p>c(u , v) = 5</p> <p>Since (0 + 5) is less than ∞, so update</p> <pre> d(v) = d(u) + c(u , v) </pre> <p>d(v) = 0 + 5 = 5</p> <p>Therefore, the distance of vertex D is 5.</p> <p>Consider the edge (B, E). Denote vertex 'B' as 'u' and vertex 'E' as 'v'. Now use the relaxing formula:</p> <p>d(u) = 6</p> <p>d(v) = ∞</p> <p>c(u , v) = -1</p> <p>Since (6 - 1) is less than ∞, so update</p> <pre> d(v) = d(u) + c(u , v) </pre> <p>d(v) = 6 - 1= 5</p> <p>Therefore, the distance of vertex E is 5.</p> <p>Consider the edge (C, E). Denote vertex 'C' as 'u' and vertex 'E' as 'v'. Now use the relaxing formula:</p> <p>d(u) = 4</p> <p>d(v) = 5</p> <p>c(u , v) = 3</p> <p>Since (4 + 3) is greater than 5, so there will be no updation. The value at vertex E is 5.</p> <p>Consider the edge (D, C). Denote vertex 'D' as 'u' and vertex 'C' as 'v'. Now use the relaxing formula:</p> <p>d(u) = 5</p> <p>d(v) = 4</p> <p>c(u , v) = -2</p> <p>Since (5 -2) is less than 4, so update</p> <pre> d(v) = d(u) + c(u , v) </pre> <p>d(v) = 5 - 2 = 3</p> <p>Therefore, the distance of vertex C is 3.</p> <p>Consider the edge (D, F). Denote vertex 'D' as 'u' and vertex 'F' as 'v'. Now use the relaxing formula:</p> <p>d(u) = 5</p> <p>d(v) = ∞</p> <p>c(u , v) = -1</p> <p>Since (5 -1) is less than ∞, so update</p> <pre> d(v) = d(u) + c(u , v) </pre> <p>d(v) = 5 - 1 = 4</p> <p>Therefore, the distance of vertex F is 4.</p> <p>Consider the edge (E, F). Denote vertex 'E' as 'u' and vertex 'F' as 'v'. Now use the relaxing formula:</p> <p>d(u) = 5</p> <p>d(v) = ∞</p> <p>c(u , v) = 3</p> <p>Since (5 + 3) is greater than 4, so there would be no updation on the distance value of vertex F.</p> <p>Consider the edge (C, B). Denote vertex 'C' as 'u' and vertex 'B' as 'v'. Now use the relaxing formula:</p> <p>d(u) = 3</p> <p>d(v) = 6</p> <p>c(u , v) = -2</p> <p>Since (3 - 2) is less than 6, so update</p> <pre> d(v) = d(u) + c(u , v) </pre> <p>d(v) = 3 - 2 = 1</p> <p>Therefore, the distance of vertex B is 1.</p> <p>Now the first iteration is completed. We move to the second iteration.</p> <p> <strong>Second iteration:</strong> </p> <p>In the second iteration, we again check all the edges. The first edge is (A, B). Since (0 + 6) is greater than 1 so there would be no updation in the vertex B.</p> <p>The next edge is (A, C). Since (0 + 4) is greater than 3 so there would be no updation in the vertex C.</p> <p>The next edge is (A, D). Since (0 + 5) equals to 5 so there would be no updation in the vertex D.</p> <p>The next edge is (B, E). Since (1 - 1) equals to 0 which is less than 5 so update:</p> <p>d(v) = d(u) + c(u, v)</p> <p>d(E) = d(B) +c(B , E)</p> <p>= 1 - 1 = 0</p> <p>The next edge is (C, E). Since (3 + 3) equals to 6 which is greater than 5 so there would be no updation in the vertex E.</p> <p>The next edge is (D, C). Since (5 - 2) equals to 3 so there would be no updation in the vertex C.</p> <p>The next edge is (D, F). Since (5 - 1) equals to 4 so there would be no updation in the vertex F.</p> <p>The next edge is (E, F). Since (5 + 3) equals to 8 which is greater than 4 so there would be no updation in the vertex F.</p> <p>The next edge is (C, B). Since (3 - 2) equals to 1` so there would be no updation in the vertex B.</p> <img src="//techcodeview.com/img/daa-tutorial/85/bellman-ford-algorithm-3.webp" alt="Bellman-Ford Algorithm"> <p> <strong>Third iteration</strong> </p> <p>We will perform the same steps as we did in the previous iterations. We will observe that there will be no updation in the distance of vertices.</p> <pre> The following are the distances of vertices: A: 0 B: 1 C: 3 D: 5 E: 0 F: 3 </pre> <p> <strong>Time Complexity</strong> </p> <p>The time complexity of Bellman ford algorithm would be O(E|V| - 1).</p> <pre> function bellmanFord(G, S) for each vertex V in G distance[V] <- 0 infinite previous[v] <- null distance[s] for each vertex v in g edge (u,v) tempdistance distance[u] + edge_weight(u, v) if < distance[v] u distance[v} error: negative cycle exists return distance[], previous[] pre> <p> <strong>Drawbacks of Bellman ford algorithm</strong> </p> <ul> <li>The bellman ford algorithm does not produce a correct answer if the sum of the edges of a cycle is negative. Let's understand this property through an example. Consider the below graph. <br> <img src="//techcodeview.com/img/daa-tutorial/85/bellman-ford-algorithm-4.webp" alt="Bellman-Ford Algorithm"></li> <li>In the above graph, we consider vertex 1 as the source vertex and provides 0 value to it. We provide infinity value to other vertices shown as below: <br> <img src="//techcodeview.com/img/daa-tutorial/85/bellman-ford-algorithm-5.webp" alt="Bellman-Ford Algorithm"> <br>Edges can be written as: <br> (1, 3), (1, 2), (2, 4), (3, 2), (4, 3) </li> </ul> <p> <strong>First iteration</strong> </p> <p> <strong>Consider the edge (1, 3). Denote vertex '1' as 'u' and vertex '3' as 'v'. Now use the relaxing formula:</strong> </p> <p>d(u) = 0</p> <p>d(v) = ∞</p> <p>c(u , v) = 5</p> <p>Since (0 + 5) is less than ∞, so update</p> <pre> d(v) = d(u) + c(u , v) </pre> <p>d(v) = 0 + 5 = 5</p> <p>Therefore, the distance of vertex 3 is 5.</p> <p> <strong>Consider the edge (1, 2). Denote vertex '1' as 'u' and vertex '2' as 'v'. Now use the relaxing formula:</strong> </p> <p>d(u) = 0</p> <p>d(v) = ∞</p> <p>c(u , v) = 4</p> <p>Since (0 + 4) is less than ∞, so update</p> <pre> d(v) = d(u) + c(u , v) </pre> <p>d(v) = 0 + 4 = 4</p> <p>Therefore, the distance of vertex 2 is 4.</p> <p> <strong>Consider the edge (3, 2). Denote vertex '3' as 'u' and vertex '2' as 'v'. Now use the relaxing formula:</strong> </p> <p>d(u) = 5</p> <p>d(v) = 4</p> <p>c(u , v) = 7</p> <p>Since (5 + 7) is greater than 4, so there would be no updation in the vertex 2.</p> <p> <strong>Consider the edge (2, 4). Denote vertex '2' as 'u' and vertex '4' as 'v'. Now use the relaxing formula:</strong> </p> <p>d(u) = 4</p> <p>d(v) = ∞</p> <p>c(u , v) = 7</p> <p>Since (4 + 7) equals to 11 which is less than ∞, so update</p> <pre> d(v) = d(u) + c(u , v) </pre> <p>d(v) = 4 + 7 = 11</p> <p>Therefore, the distance of vertex 4 is 11.</p> <p> <strong>Consider the edge (4, 3). Denote vertex '4' as 'u' and vertex '3' as 'v'. Now use the relaxing formula:</strong> </p> <p>d(u) = 11</p> <p>d(v) = 5</p> <p>c(u , v) = -15</p> <p>Since (11 - 15) equals to -4 which is less than 5, so update</p> <pre> d(v) = d(u) + c(u , v) </pre> <p>d(v) = 11 - 15 = -4</p> <p>Therefore, the distance of vertex 3 is -4.</p> <p>Now we move to the second iteration.</p> <p> <strong>Second iteration</strong> </p> <p>Now, again we will check all the edges. The first edge is (1, 3). Since (0 + 5) equals to 5 which is greater than -4 so there would be no updation in the vertex 3.</p> <p>The next edge is (1, 2). Since (0 + 4) equals to 4 so there would be no updation in the vertex 2.</p> <p>The next edge is (3, 2). Since (-4 + 7) equals to 3 which is less than 4 so update:</p> <p>d(v) = d(u) + c(u, v)</p> <p>d(2) = d(3) +c(3, 2)</p> <p>= -4 + 7 = 3</p> <p>Therefore, the value at vertex 2 is 3.</p> <p>The next edge is (2, 4). Since ( 3+7) equals to 10 which is less than 11 so update</p> <p>d(v) = d(u) + c(u, v)</p> <p>d(4) = d(2) +c(2, 4)</p> <p>= 3 + 7 = 10</p> <p>Therefore, the value at vertex 4 is 10.</p> <p>The next edge is (4, 3). Since (10 - 15) equals to -5 which is less than -4 so update:</p> <p>d(v) = d(u) + c(u, v)</p> <p>d(3) = d(4) +c(4, 3)</p> <p>= 10 - 15 = -5</p> <p>Therefore, the value at vertex 3 is -5.</p> <p>Now we move to the third iteration.</p> <p> <strong>Third iteration</strong> </p> <p>Now again we will check all the edges. The first edge is (1, 3). Since (0 + 5) equals to 5 which is greater than -5 so there would be no updation in the vertex 3.</p> <p>The next edge is (1, 2). Since (0 + 4) equals to 4 which is greater than 3 so there would be no updation in the vertex 2.</p> <p>The next edge is (3, 2). Since (-5 + 7) equals to 2 which is less than 3 so update:</p> <p>d(v) = d(u) + c(u, v)</p> <p>d(2) = d(3) +c(3, 2)</p> <p>= -5 + 7 = 2</p> <p>Therefore, the value at vertex 2 is 2.</p> <p>The next edge is (2, 4). Since (2 + 7) equals to 9 which is less than 10 so update:</p> <p>d(v) = d(u) + c(u, v)</p> <p>d(4) = d(2) +c(2, 4)</p> <p>= 2 + 7 = 9</p> <p>Therefore, the value at vertex 4 is 9.</p> <p>The next edge is (4, 3). Since (9 - 15) equals to -6 which is less than -5 so update:</p> <p>d(v) = d(u) + c(u, v)</p> <p>d(3) = d(4) +c(4, 3)</p> <p>= 9 - 15 = -6</p> <p>Therefore, the value at vertex 3 is -6.</p> <img src="//techcodeview.com/img/daa-tutorial/85/bellman-ford-algorithm-6.webp" alt="Bellman-Ford Algorithm"> <p>Since the graph contains 4 vertices, so according to the bellman ford algorithm, there would be only 3 iterations. If we try to perform 4<sup>th</sup> iteration on the graph, the distance of the vertices from the given vertex should not change. If the distance varies, it means that the bellman ford algorithm is not providing the correct answer.</p> <p> <strong>4<sup>th</sup> iteration</strong> </p> <p>The first edge is (1, 3). Since (0 +5) equals to 5 which is greater than -6 so there would be no change in the vertex 3.</p> <p>The next edge is (1, 2). Since (0 + 4) is greater than 2 so there would be no updation.</p> <p>The next edge is (3, 2). Since (-6 + 7) equals to 1 which is less than 3 so update:</p> <p>d(v) = d(u) + c(u, v)</p> <p>d(2) = d(3) +c(3, 2)</p> <p>= -6 + 7 = 1</p> <p>In this case, the value of the vertex is updated. So, we conclude that the bellman ford algorithm does not work when the graph contains the negative weight cycle.</p> <p>Therefore, the value at vertex 2 is 1.</p> <hr></-></pre></d(v))>
d(v) = 0 + 6 = 6
לכן, המרחק של קודקוד B הוא 6.
שקול את הקצה (A, C). סמן את קודקוד 'A' בתור 'u' וקודקוד 'C' כ-'v'. כעת השתמש בנוסחה המרגיעה:
d(u) = 0
d(v) = ∞
c(u ,v) = 4
מכיוון ש-(0 + 4) קטן מ-∞, אז עדכן
d(v) = d(u) + c(u , v)
d(v) = 0 + 4 = 4
לכן, המרחק של קודקוד C הוא 4.
שקול את הקצה (A, D). סמן את קודקוד 'A' בתור 'u' וקודקוד 'D' כ-'v'. כעת השתמש בנוסחה המרגיעה:
d(u) = 0
d(v) = ∞
c(u ,v) = 5
מכיוון ש-(0 + 5) קטן מ-∞, אז עדכן
d(v) = d(u) + c(u , v)
d(v) = 0 + 5 = 5
לכן, המרחק של קודקוד D הוא 5.
שקול את הקצה (B, E). סמן את קודקוד 'B' בתור 'u' וקודקוד 'E' כ-'v'. כעת השתמש בנוסחה המרגיעה:
d(u) = 6
d(v) = ∞
c(u, v) = -1
מכיוון ש-(6 - 1) קטן מ-∞, אז עדכן
d(v) = d(u) + c(u , v)
d(v) = 6 - 1= 5
לכן, המרחק של קודקוד E הוא 5.
שקול את הקצה (C, E). סמן את קודקוד 'C' בתור 'u' וקודקוד 'E' כ-'v'. כעת השתמש בנוסחה המרגיעה:
d(u) = 4
d(v) = 5
c(u ,v) = 3
מכיוון ש-(4 + 3) גדול מ-5, אז לא יהיה עדכון. הערך בקודקוד E הוא 5.
שקול את הקצה (D, C). סמן את קודקוד 'D' בתור 'u' וקודקוד 'C' כ-'v'. כעת השתמש בנוסחה המרגיעה:
d(u) = 5
d(v) = 4
c(u, v) = -2
מכיוון ש-(5 -2) הוא פחות מ-4, אז עדכן
d(v) = d(u) + c(u , v)
d(v) = 5 - 2 = 3
לכן, המרחק של קודקוד C הוא 3.
שקול את הקצה (D, F). סמן את קודקוד 'D' בתור 'u' וקודקוד 'F' כ-'v'. כעת השתמש בנוסחה המרגיעה:
d(u) = 5
d(v) = ∞
c(u, v) = -1
מכיוון ש-(5 -1) קטן מ-∞, אז עדכן
d(v) = d(u) + c(u , v)
d(v) = 5 - 1 = 4
לכן, המרחק של קודקוד F הוא 4.
שקול את הקצה (E, F). סמן את הקודקוד 'E' בתור 'u' וקודקוד 'F' כ-'v'. כעת השתמש בנוסחה המרגיעה:
d(u) = 5
d(v) = ∞
c(u ,v) = 3
מכיוון ש-(5 + 3) גדול מ-4, אז לא יהיה עדכון בערך המרחק של קודקוד F.
שקול את הקצה (C, B). סמן את קודקוד 'C' בתור 'u' וקודקוד 'B' כ-'v'. כעת השתמש בנוסחה המרגיעה:
d(u) = 3
d(v) = 6
c(u, v) = -2
מכיוון ש-(3 - 2) הוא פחות מ-6, אז עדכן
d(v) = d(u) + c(u , v)
d(v) = 3 - 2 = 1
לכן, המרחק של קודקוד B הוא 1.
בתים ל-python מחרוזת
כעת האיטרציה הראשונה הושלמה. נעבור לאיטרציה השנייה.
איטרציה שנייה:
באיטרציה השנייה, אנו שוב בודקים את כל הקצוות. הקצה הראשון הוא (A, B). מכיוון ש-(0 + 6) גדול מ-1 אז לא יהיה עדכון בקודקוד B.
הקצה הבא הוא (A, C). מכיוון ש-(0 + 4) גדול מ-3 אז לא יהיה עדכון בקודקוד C.
הקצה הבא הוא (A, D). מכיוון ש(0 + 5) שווה ל-5 אז לא יהיה עדכון בקודקוד D.
הקצה הבא הוא (B, E). מכיוון ש-(1 - 1) שווה ל-0 שהוא פחות מ-5 אז עדכן:
d(v) = d(u) + c(u, v)
d(E) = d(B) +c(B , E)
= 1 - 1 = 0
הקצה הבא הוא (C, E). מכיוון ש-(3 + 3) שווה ל-6 שהוא גדול מ-5 אז לא יהיה עדכון בקודקוד E.
הקצה הבא הוא (D, C). מכיוון ש(5 - 2) שווה ל-3 אז לא יהיה עדכון בקודקוד C.
הקצה הבא הוא (D, F). מאז (5 - 1) שווה ל-4 אז לא יהיה עדכון בקודקוד F.
הקצה הבא הוא (E, F). מכיוון ש(5 + 3) שווה ל-8 שהוא גדול מ-4 אז לא יהיה עדכון בקודקוד F.
הקצה הבא הוא (C, B). מכיוון ש-(3 - 2) שווה ל-1` אז לא יהיה עדכון בקודקוד B.

איטרציה שלישית
נבצע את אותם שלבים כמו שעשינו באיטרציות הקודמות. נבחין שלא יהיה עדכון במרחק של קודקודים.
The following are the distances of vertices: A: 0 B: 1 C: 3 D: 5 E: 0 F: 3
מורכבות זמן
מורכבות הזמן של אלגוריתם בלמן פורד תהיה O(E|V| - 1).
function bellmanFord(G, S) for each vertex V in G distance[V] <- 0 infinite previous[v] <- null distance[s] for each vertex v in g edge (u,v) tempdistance distance[u] + edge_weight(u, v) if < distance[v] u distance[v} error: negative cycle exists return distance[], previous[] pre> <p> <strong>Drawbacks of Bellman ford algorithm</strong> </p> <ul> <li>The bellman ford algorithm does not produce a correct answer if the sum of the edges of a cycle is negative. Let's understand this property through an example. Consider the below graph. <br> <img src="//techcodeview.com/img/daa-tutorial/85/bellman-ford-algorithm-4.webp" alt="Bellman-Ford Algorithm"></li> <li>In the above graph, we consider vertex 1 as the source vertex and provides 0 value to it. We provide infinity value to other vertices shown as below: <br> <img src="//techcodeview.com/img/daa-tutorial/85/bellman-ford-algorithm-5.webp" alt="Bellman-Ford Algorithm"> <br>Edges can be written as: <br> (1, 3), (1, 2), (2, 4), (3, 2), (4, 3) </li> </ul> <p> <strong>First iteration</strong> </p> <p> <strong>Consider the edge (1, 3). Denote vertex '1' as 'u' and vertex '3' as 'v'. Now use the relaxing formula:</strong> </p> <p>d(u) = 0</p> <p>d(v) = ∞</p> <p>c(u , v) = 5</p> <p>Since (0 + 5) is less than ∞, so update</p> <pre> d(v) = d(u) + c(u , v) </pre> <p>d(v) = 0 + 5 = 5</p> <p>Therefore, the distance of vertex 3 is 5.</p> <p> <strong>Consider the edge (1, 2). Denote vertex '1' as 'u' and vertex '2' as 'v'. Now use the relaxing formula:</strong> </p> <p>d(u) = 0</p> <p>d(v) = ∞</p> <p>c(u , v) = 4</p> <p>Since (0 + 4) is less than ∞, so update</p> <pre> d(v) = d(u) + c(u , v) </pre> <p>d(v) = 0 + 4 = 4</p> <p>Therefore, the distance of vertex 2 is 4.</p> <p> <strong>Consider the edge (3, 2). Denote vertex '3' as 'u' and vertex '2' as 'v'. Now use the relaxing formula:</strong> </p> <p>d(u) = 5</p> <p>d(v) = 4</p> <p>c(u , v) = 7</p> <p>Since (5 + 7) is greater than 4, so there would be no updation in the vertex 2.</p> <p> <strong>Consider the edge (2, 4). Denote vertex '2' as 'u' and vertex '4' as 'v'. Now use the relaxing formula:</strong> </p> <p>d(u) = 4</p> <p>d(v) = ∞</p> <p>c(u , v) = 7</p> <p>Since (4 + 7) equals to 11 which is less than ∞, so update</p> <pre> d(v) = d(u) + c(u , v) </pre> <p>d(v) = 4 + 7 = 11</p> <p>Therefore, the distance of vertex 4 is 11.</p> <p> <strong>Consider the edge (4, 3). Denote vertex '4' as 'u' and vertex '3' as 'v'. Now use the relaxing formula:</strong> </p> <p>d(u) = 11</p> <p>d(v) = 5</p> <p>c(u , v) = -15</p> <p>Since (11 - 15) equals to -4 which is less than 5, so update</p> <pre> d(v) = d(u) + c(u , v) </pre> <p>d(v) = 11 - 15 = -4</p> <p>Therefore, the distance of vertex 3 is -4.</p> <p>Now we move to the second iteration.</p> <p> <strong>Second iteration</strong> </p> <p>Now, again we will check all the edges. The first edge is (1, 3). Since (0 + 5) equals to 5 which is greater than -4 so there would be no updation in the vertex 3.</p> <p>The next edge is (1, 2). Since (0 + 4) equals to 4 so there would be no updation in the vertex 2.</p> <p>The next edge is (3, 2). Since (-4 + 7) equals to 3 which is less than 4 so update:</p> <p>d(v) = d(u) + c(u, v)</p> <p>d(2) = d(3) +c(3, 2)</p> <p>= -4 + 7 = 3</p> <p>Therefore, the value at vertex 2 is 3.</p> <p>The next edge is (2, 4). Since ( 3+7) equals to 10 which is less than 11 so update</p> <p>d(v) = d(u) + c(u, v)</p> <p>d(4) = d(2) +c(2, 4)</p> <p>= 3 + 7 = 10</p> <p>Therefore, the value at vertex 4 is 10.</p> <p>The next edge is (4, 3). Since (10 - 15) equals to -5 which is less than -4 so update:</p> <p>d(v) = d(u) + c(u, v)</p> <p>d(3) = d(4) +c(4, 3)</p> <p>= 10 - 15 = -5</p> <p>Therefore, the value at vertex 3 is -5.</p> <p>Now we move to the third iteration.</p> <p> <strong>Third iteration</strong> </p> <p>Now again we will check all the edges. The first edge is (1, 3). Since (0 + 5) equals to 5 which is greater than -5 so there would be no updation in the vertex 3.</p> <p>The next edge is (1, 2). Since (0 + 4) equals to 4 which is greater than 3 so there would be no updation in the vertex 2.</p> <p>The next edge is (3, 2). Since (-5 + 7) equals to 2 which is less than 3 so update:</p> <p>d(v) = d(u) + c(u, v)</p> <p>d(2) = d(3) +c(3, 2)</p> <p>= -5 + 7 = 2</p> <p>Therefore, the value at vertex 2 is 2.</p> <p>The next edge is (2, 4). Since (2 + 7) equals to 9 which is less than 10 so update:</p> <p>d(v) = d(u) + c(u, v)</p> <p>d(4) = d(2) +c(2, 4)</p> <p>= 2 + 7 = 9</p> <p>Therefore, the value at vertex 4 is 9.</p> <p>The next edge is (4, 3). Since (9 - 15) equals to -6 which is less than -5 so update:</p> <p>d(v) = d(u) + c(u, v)</p> <p>d(3) = d(4) +c(4, 3)</p> <p>= 9 - 15 = -6</p> <p>Therefore, the value at vertex 3 is -6.</p> <img src="//techcodeview.com/img/daa-tutorial/85/bellman-ford-algorithm-6.webp" alt="Bellman-Ford Algorithm"> <p>Since the graph contains 4 vertices, so according to the bellman ford algorithm, there would be only 3 iterations. If we try to perform 4<sup>th</sup> iteration on the graph, the distance of the vertices from the given vertex should not change. If the distance varies, it means that the bellman ford algorithm is not providing the correct answer.</p> <p> <strong>4<sup>th</sup> iteration</strong> </p> <p>The first edge is (1, 3). Since (0 +5) equals to 5 which is greater than -6 so there would be no change in the vertex 3.</p> <p>The next edge is (1, 2). Since (0 + 4) is greater than 2 so there would be no updation.</p> <p>The next edge is (3, 2). Since (-6 + 7) equals to 1 which is less than 3 so update:</p> <p>d(v) = d(u) + c(u, v)</p> <p>d(2) = d(3) +c(3, 2)</p> <p>= -6 + 7 = 1</p> <p>In this case, the value of the vertex is updated. So, we conclude that the bellman ford algorithm does not work when the graph contains the negative weight cycle.</p> <p>Therefore, the value at vertex 2 is 1.</p> <hr></->
d(v) = 0 + 5 = 5
לכן, המרחק של קודקוד 3 הוא 5.
שקול את הקצה (1, 2). סמן את הקודקוד '1' בתור 'u' וקודקוד '2' כ-'v'. כעת השתמש בנוסחה המרגיעה:
d(u) = 0
d(v) = ∞
c(u ,v) = 4
מכיוון ש-(0 + 4) קטן מ-∞, אז עדכן
d(v) = d(u) + c(u , v)
d(v) = 0 + 4 = 4
לכן, המרחק של קודקוד 2 הוא 4.
שקול את הקצה (3, 2). סמן את הקודקוד '3' בתור 'u' וקודקוד '2' כ-'v'. כעת השתמש בנוסחה המרגיעה:
d(u) = 5
d(v) = 4
c(u, v) = 7
מכיוון ש-(5 + 7) גדול מ-4, אז לא יהיה עדכון בקודקוד 2.
שקול את הקצה (2, 4). סמן את הקודקוד '2' בתור 'u' וקודקוד '4' בתור 'v'. כעת השתמש בנוסחה המרגיעה:
d(u) = 4
d(v) = ∞
c(u, v) = 7
מכיוון ש-(4 + 7) שווה ל-11 שהוא פחות מ-∞, אז עדכן
d(v) = d(u) + c(u , v)
d(v) = 4 + 7 = 11
לכן, המרחק של קודקוד 4 הוא 11.
שקול את הקצה (4, 3). סמן את הקודקוד '4' בתור 'u' וקודקוד '3' כ-'v'. כעת השתמש בנוסחה המרגיעה:
d(u) = 11
d(v) = 5
c(u, v) = -15
מכיוון ש-(11 - 15) שווה ל-4 שהוא פחות מ-5, אז עדכן
d(v) = d(u) + c(u , v)
d(v) = 11 - 15 = -4
לכן, המרחק של קודקוד 3 הוא -4.
כעת נעבור לאיטרציה השנייה.
איטרציה שנייה
כעת, שוב נבדוק את כל הקצוות. הקצה הראשון הוא (1, 3). מכיוון ש-(0 + 5) שווה ל-5 שהוא גדול מ-4 אז לא יהיה עדכון בקודקוד 3.
android.process.acore ממשיך לעצור
הקצה הבא הוא (1, 2). מכיוון ש-(0 + 4) שווה ל-4 אז לא יהיה עדכון בקודקוד 2.
הקצה הבא הוא (3, 2). מכיוון ש-(-4 + 7) שווה ל-3 שהוא פחות מ-4 אז עדכן:
d(v) = d(u) + c(u, v)
d(2) = d(3) +c(3, 2)
= -4 + 7 = 3
לכן, הערך בקודקוד 2 הוא 3.
הקצה הבא הוא (2, 4). מאז (3+7) שווה ל-10 שזה פחות מ-11 אז עדכן
d(v) = d(u) + c(u, v)
d(4) = d(2) +c(2, 4)
= 3 + 7 = 10
לכן, הערך בקודקוד 4 הוא 10.
גראנדרה
הקצה הבא הוא (4, 3). מכיוון ש-(10 - 15) שווה ל-5 שהוא פחות מ-4 אז עדכן:
d(v) = d(u) + c(u, v)
d(3) = d(4) +c(4, 3)
= 10 - 15 = -5
לכן, הערך בקודקוד 3 הוא -5.
כעת נעבור לאיטרציה השלישית.
איטרציה שלישית
עכשיו שוב נבדוק את כל הקצוות. הקצה הראשון הוא (1, 3). מכיוון ש-(0 + 5) שווה ל-5 שהוא גדול מ-5 אז לא יהיה עדכון בקודקוד 3.
הקצה הבא הוא (1, 2). מכיוון ש-(0 + 4) שווה ל-4 שהוא גדול מ-3 אז לא יהיה עדכון בקודקוד 2.
הקצה הבא הוא (3, 2). מכיוון ש-(-5 + 7) שווה ל-2 שזה פחות מ-3 אז עדכן:
d(v) = d(u) + c(u, v)
d(2) = d(3) +c(3, 2)
= -5 + 7 = 2
לכן, הערך בקודקוד 2 הוא 2.
הקצה הבא הוא (2, 4). מכיוון ש-(2 + 7) שווה ל-9 שזה פחות מ-10 אז עדכן:
d(v) = d(u) + c(u, v)
d(4) = d(2) +c(2, 4)
= 2 + 7 = 9
לכן, הערך בקודקוד 4 הוא 9.
הקצה הבא הוא (4, 3). מכיוון ש-(9 - 15) שווה ל-6 שהוא פחות מ-5 אז עדכן:
d(v) = d(u) + c(u, v)
d(3) = d(4) +c(4, 3)
= 9 - 15 = -6
לכן, הערך בקודקוד 3 הוא -6.

מכיוון שהגרף מכיל 4 קודקודים, אז לפי אלגוריתם בלמן פורד, יהיו רק 3 איטרציות. אם ננסה לבצע 4ה'איטרציה על הגרף, המרחק של הקודקודים מהקודקוד הנתון לא אמור להשתנות. אם המרחק משתנה, זה אומר שאלגוריתם בלמן פורד אינו מספק את התשובה הנכונה.
4ה'איטרציה
הקצה הראשון הוא (1, 3). מכיוון ש-(0 +5) שווה ל-5 שהוא גדול מ-6 אז לא יהיה שינוי בקודקוד 3.
הקצה הבא הוא (1, 2). מכיוון ש-(0 + 4) גדול מ-2 אז לא יהיה עדכון.
הקצה הבא הוא (3, 2). מכיוון ש-(-6 + 7) שווה ל-1 שהוא פחות מ-3 אז עדכן:
d(v) = d(u) + c(u, v)
d(2) = d(3) +c(3, 2)
= -6 + 7 = 1
במקרה זה, ערך הקודקוד מתעדכן. לכן, אנו מסיקים שאלגוריתם בלמן פורד אינו פועל כאשר הגרף מכיל את מחזור המשקל השלילי.
לכן, הערך בקודקוד 2 הוא 1.
