ניתן להגדיר מערך דו מימדי כמערך של מערכים. המערך הדו-ממדי מאורגן כמטריצות שיכולות להיות מיוצגות כאוסף של שורות ועמודות.
עם זאת, מערכים דו-ממדיים נוצרים כדי ליישם מבנה נתונים דומה לבסיס נתונים יחסי. זה מספק קלות להחזיק כמות גדולה של נתונים בבת אחת, שניתן להעביר לכל מספר פונקציות בכל מקום שנדרש.
כיצד להכריז על מערך 2D
התחביר של הכרזת מערך דו-ממדי דומה מאוד לזה של מערך חד-ממדי, שניתן כדלקמן.
המרת מחרוזת ל-int java
int arr[max_rows][max_columns];
עם זאת, זה מייצר את מבנה הנתונים שנראה כמו הבא.
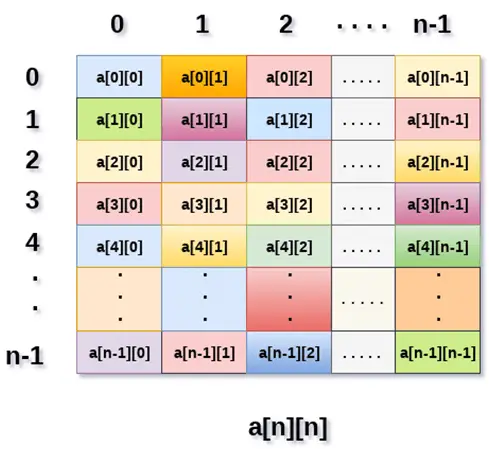
התמונה למעלה מציגה את המערך הדו מימדי, האלמנטים מאורגנים בצורה של שורות ועמודות. האלמנט הראשון בשורה הראשונה מיוצג על ידי a[0][0] כאשר המספר המוצג באינדקס הראשון הוא המספר של אותה שורה ואילו המספר המוצג באינדקס השני הוא מספר העמודה.
כיצד אנו ניגשים לנתונים במערך דו מימדי
בשל העובדה שניתן לגשת אקראית לאלמנטים של מערכים דו מימדיים. בדומה למערכים חד מימדיים, אנו יכולים לגשת לתאים בודדים במערך דו-ממדי על ידי שימוש במדדים של התאים. ישנם שני מדדים המחוברים לתא מסוים, האחד הוא מספר השורה שלו ואילו השני הוא מספר העמודה שלו.
עם זאת, אנו יכולים לאחסן את הערך המאוחסן בכל תא מסוים של מערך דו-ממדי למשתנה x כלשהו באמצעות התחביר הבא.
int x = a[i][j];
כאשר i ו-j הם מספר השורה והעמודה של התא בהתאמה.
אנו יכולים להקצות כל תא של מערך דו-ממדי ל-0 באמצעות הקוד הבא:
for ( int i=0; i<n ;i++) { for (int j="0;" j<n; j++) a[i][j]="0;" } < pre> <h2>Initializing 2D Arrays </h2> <p>We know that, when we declare and initialize one dimensional array in C programming simultaneously, we don't need to specify the size of the array. However this will not work with 2D arrays. We will have to define at least the second dimension of the array. </p> <p>The syntax to declare and initialize the 2D array is given as follows. </p> <pre> int arr[2][2] = {0,1,2,3}; </pre> <p>The number of elements that can be present in a 2D array will always be equal to ( <strong>number of rows * number of columns</strong> ). </p> <p> <strong>Example :</strong> Storing User's data into a 2D array and printing it. </p> <p> <strong>C Example : </strong> </p> <pre> #include void main () { int arr[3][3],i,j; for (i=0;i<3;i++) { for (j="0;j<3;j++)" printf('enter a[%d][%d]: ',i,j); scanf('%d',&arr[i][j]); } printf('
printing the elements ....
'); for(i="0;i<3;i++)" printf('
'); printf('%d ',arr[i][j]); < pre> <h3>Java Example</h3> <pre> import java.util.Scanner; publicclass TwoDArray { publicstaticvoid main(String[] args) { int[][] arr = newint[3][3]; Scanner sc = new Scanner(System.in); for (inti =0;i<3;i++) { for(intj="0;j<3;j++)" system.out.print('enter element'); arr[i][j]="sc.nextInt();" system.out.println(); } system.out.println('printing elements...'); for(inti="0;i<3;i++)" system.out.print(arr[i][j]+' '); < pre> <h3>C# Example </h3> <pre> using System; public class Program { public static void Main() { int[,] arr = new int[3,3]; for (int i=0;i<3;i++) { for (int j="0;j<3;j++)" console.writeline('enter element'); arr[i,j]="Convert.ToInt32(Console.ReadLine());" } console.writeline('printing elements...'); i="0;i<3;i++)" console.writeline(); console.write(arr[i,j]+' '); < pre> <h2>Mapping 2D array to 1D array </h2> <p>When it comes to map a 2 dimensional array, most of us might think that why this mapping is required. However, 2 D arrays exists from the user point of view. 2D arrays are created to implement a relational database table lookalike data structure, in computer memory, the storage technique for 2D array is similar to that of an one dimensional array. </p> <p>The size of a two dimensional array is equal to the multiplication of number of rows and the number of columns present in the array. We do need to map two dimensional array to the one dimensional array in order to store them in the memory.</p> <p>A 3 X 3 two dimensional array is shown in the following image. However, this array needs to be mapped to a one dimensional array in order to store it into the memory. </p> <br> <img src="//techcodeview.com/img/ds-tutorial/80/2d-array-2.webp" alt="DS 2D Array"> <br> <p>There are two main techniques of storing 2D array elements into memory </p> <h3>1. Row Major ordering </h3> <p>In row major ordering, all the rows of the 2D array are stored into the memory contiguously. Considering the array shown in the above image, its memory allocation according to row major order is shown as follows. </p> <br> <img src="//techcodeview.com/img/ds-tutorial/80/2d-array-3.webp" alt="DS 2D Array"> <br> <p>first, the 1<sup>st</sup> row of the array is stored into the memory completely, then the 2<sup>nd</sup> row of the array is stored into the memory completely and so on till the last row.</p> <br> <img src="//techcodeview.com/img/ds-tutorial/80/2d-array-4.webp" alt="DS 2D Array"> <br> <h3>2. Column Major ordering </h3> <p>According to the column major ordering, all the columns of the 2D array are stored into the memory contiguously. The memory allocation of the array which is shown in in the above image is given as follows.</p> <br> <img src="//techcodeview.com/img/ds-tutorial/80/2d-array-5.webp" alt="DS 2D Array"> <br> <p>first, the 1<sup>st</sup> column of the array is stored into the memory completely, then the 2<sup>nd</sup> row of the array is stored into the memory completely and so on till the last column of the array. </p> <br> <img src="//techcodeview.com/img/ds-tutorial/80/2d-array-6.webp" alt="DS 2D Array"> <br> <h2>Calculating the Address of the random element of a 2D array </h2> <p>Due to the fact that, there are two different techniques of storing the two dimensional array into the memory, there are two different formulas to calculate the address of a random element of the 2D array. </p> <h3>By Row Major Order </h3> <p>If array is declared by a[m][n] where m is the number of rows while n is the number of columns, then address of an element a[i][j] of the array stored in row major order is calculated as, </p> <pre> Address(a[i][j]) = B. A. + (i * n + j) * size </pre> <p>where, B. A. is the base address or the address of the first element of the array a[0][0] . </p> <p> <strong>Example : </strong> </p> <pre> a[10...30, 55...75], base address of the array (BA) = 0, size of an element = 4 bytes . Find the location of a[15][68]. Address(a[15][68]) = 0 + ((15 - 10) x (68 - 55 + 1) + (68 - 55)) x 4 = (5 x 14 + 13) x 4 = 83 x 4 = 332 answer </pre> <h3>By Column major order </h3> <p>If array is declared by a[m][n] where m is the number of rows while n is the number of columns, then address of an element a[i][j] of the array stored in row major order is calculated as, </p> <pre> Address(a[i][j]) = ((j*m)+i)*Size + BA </pre> <p>where BA is the base address of the array. </p> <p> <strong>Example:</strong> </p> <pre> A [-5 ... +20][20 ... 70], BA = 1020, Size of element = 8 bytes. Find the location of a[0][30]. Address [A[0][30]) = ((30-20) x 24 + 5) x 8 + 1020 = 245 x 8 + 1020 = 2980 bytes </pre> <hr></3;i++)></pre></3;i++)></pre></3;i++)></pre></n> מספר האלמנטים שיכולים להיות נוכחים במערך דו מימדי יהיה תמיד שווה ל- ( מספר שורות * מספר עמודות ).
דוגמא : אחסון נתוני המשתמש במערך דו מימדי והדפסתם.
C דוגמה:
#include void main () { int arr[3][3],i,j; for (i=0;i<3;i++) { for (j="0;j<3;j++)" printf(\'enter a[%d][%d]: \',i,j); scanf(\'%d\',&arr[i][j]); } printf(\'
printing the elements ....
\'); for(i="0;i<3;i++)" printf(\'
\'); printf(\'%d \',arr[i][j]); < pre> <h3>Java Example</h3> <pre> import java.util.Scanner; publicclass TwoDArray { publicstaticvoid main(String[] args) { int[][] arr = newint[3][3]; Scanner sc = new Scanner(System.in); for (inti =0;i<3;i++) { for(intj="0;j<3;j++)" system.out.print(\'enter element\'); arr[i][j]="sc.nextInt();" system.out.println(); } system.out.println(\'printing elements...\'); for(inti="0;i<3;i++)" system.out.print(arr[i][j]+\' \'); < pre> <h3>C# Example </h3> <pre> using System; public class Program { public static void Main() { int[,] arr = new int[3,3]; for (int i=0;i<3;i++) { for (int j="0;j<3;j++)" console.writeline(\'enter element\'); arr[i,j]="Convert.ToInt32(Console.ReadLine());" } console.writeline(\'printing elements...\'); i="0;i<3;i++)" console.writeline(); console.write(arr[i,j]+\' \'); < pre> <h2>Mapping 2D array to 1D array </h2> <p>When it comes to map a 2 dimensional array, most of us might think that why this mapping is required. However, 2 D arrays exists from the user point of view. 2D arrays are created to implement a relational database table lookalike data structure, in computer memory, the storage technique for 2D array is similar to that of an one dimensional array. </p> <p>The size of a two dimensional array is equal to the multiplication of number of rows and the number of columns present in the array. We do need to map two dimensional array to the one dimensional array in order to store them in the memory.</p> <p>A 3 X 3 two dimensional array is shown in the following image. However, this array needs to be mapped to a one dimensional array in order to store it into the memory. </p> <br> <img src="//techcodeview.com/img/ds-tutorial/80/2d-array-2.webp" alt="DS 2D Array"> <br> <p>There are two main techniques of storing 2D array elements into memory </p> <h3>1. Row Major ordering </h3> <p>In row major ordering, all the rows of the 2D array are stored into the memory contiguously. Considering the array shown in the above image, its memory allocation according to row major order is shown as follows. </p> <br> <img src="//techcodeview.com/img/ds-tutorial/80/2d-array-3.webp" alt="DS 2D Array"> <br> <p>first, the 1<sup>st</sup> row of the array is stored into the memory completely, then the 2<sup>nd</sup> row of the array is stored into the memory completely and so on till the last row.</p> <br> <img src="//techcodeview.com/img/ds-tutorial/80/2d-array-4.webp" alt="DS 2D Array"> <br> <h3>2. Column Major ordering </h3> <p>According to the column major ordering, all the columns of the 2D array are stored into the memory contiguously. The memory allocation of the array which is shown in in the above image is given as follows.</p> <br> <img src="//techcodeview.com/img/ds-tutorial/80/2d-array-5.webp" alt="DS 2D Array"> <br> <p>first, the 1<sup>st</sup> column of the array is stored into the memory completely, then the 2<sup>nd</sup> row of the array is stored into the memory completely and so on till the last column of the array. </p> <br> <img src="//techcodeview.com/img/ds-tutorial/80/2d-array-6.webp" alt="DS 2D Array"> <br> <h2>Calculating the Address of the random element of a 2D array </h2> <p>Due to the fact that, there are two different techniques of storing the two dimensional array into the memory, there are two different formulas to calculate the address of a random element of the 2D array. </p> <h3>By Row Major Order </h3> <p>If array is declared by a[m][n] where m is the number of rows while n is the number of columns, then address of an element a[i][j] of the array stored in row major order is calculated as, </p> <pre> Address(a[i][j]) = B. A. + (i * n + j) * size </pre> <p>where, B. A. is the base address or the address of the first element of the array a[0][0] . </p> <p> <strong>Example : </strong> </p> <pre> a[10...30, 55...75], base address of the array (BA) = 0, size of an element = 4 bytes . Find the location of a[15][68]. Address(a[15][68]) = 0 + ((15 - 10) x (68 - 55 + 1) + (68 - 55)) x 4 = (5 x 14 + 13) x 4 = 83 x 4 = 332 answer </pre> <h3>By Column major order </h3> <p>If array is declared by a[m][n] where m is the number of rows while n is the number of columns, then address of an element a[i][j] of the array stored in row major order is calculated as, </p> <pre> Address(a[i][j]) = ((j*m)+i)*Size + BA </pre> <p>where BA is the base address of the array. </p> <p> <strong>Example:</strong> </p> <pre> A [-5 ... +20][20 ... 70], BA = 1020, Size of element = 8 bytes. Find the location of a[0][30]. Address [A[0][30]) = ((30-20) x 24 + 5) x 8 + 1020 = 245 x 8 + 1020 = 2980 bytes </pre> <hr></3;i++)></pre></3;i++)></pre></3;i++)> כאשר, B.A. היא כתובת הבסיס או הכתובת של האלמנט הראשון של המערך a[0][0] .
דוגמא :
a[10...30, 55...75], base address of the array (BA) = 0, size of an element = 4 bytes . Find the location of a[15][68]. Address(a[15][68]) = 0 + ((15 - 10) x (68 - 55 + 1) + (68 - 55)) x 4 = (5 x 14 + 13) x 4 = 83 x 4 = 332 answer
לפי הזמנה מרכזית בטור
אם מערך מוכרז על ידי a[m][n] כאשר m הוא מספר השורות בעוד n הוא מספר העמודות, הכתובת של אלמנט a[i][j] של המערך המאוחסן בסדר ראשי בשורה מחושבת כ- ,
קפיץ mvc
Address(a[i][j]) = ((j*m)+i)*Size + BA
כאשר BA היא כתובת הבסיס של המערך.
דוגמא:
A [-5 ... +20][20 ... 70], BA = 1020, Size of element = 8 bytes. Find the location of a[0][30]. Address [A[0][30]) = ((30-20) x 24 + 5) x 8 + 1020 = 245 x 8 + 1020 = 2980 bytes
